Моделирование и анализ данных
2019. Том 9. № 4. С. 32–45
doi:10.17759/mda.2019090402
ISSN: 2219-3758 / 2311-9454 (online)
Анализ модели выполнения производственного задания при нечеткой информации о коэффициентах прямых затрат и конечном спросе на продукцию
Аннотация
Общая информация
Ключевые слова: Нечеткая логика, треугольные числа, полностью нечеткая линейная система алгебраических уравнений, программное обеспечение
Рубрика издания: Математическое моделирование
Тип материала: научная статья
DOI: https://doi.org/10.17759/mda.2019090402
Для цитаты: Пантелеев А.В., Савельева В.С. Анализ модели выполнения производственного задания при нечеткой информации о коэффициентах прямых затрат и конечном спросе на продукцию // Моделирование и анализ данных. 2019. Том 9. № 4. С. 32–45. DOI: 10.17759/mda.2019090402
Полный текст
В статье рассматривается формирование и исследование математической модели выполнения производственного задания при наличии нечеткой информации о матрицах прямых затрат и конечного спроса. Под решением задачи с нечеткой информацией понимается решение линейной системы уравнений с нечеткой матрицей и нечеткой правой частью, описываемых с помощью нечетких треугольных чисел в форме отклонений от среднего значения. В данной задаче поиска межотраслевого баланса применяется метод LU-разложения для матрицы прямых затрат, который далее используется для решения системы линейных уравнений. Описана программная реализация численного метода поиска сильного решения полностью нечеткой системы линейных алгебраических уравнений, состоящая из двух последовательных этапов. На первом этапе проверяются необходимые и достаточные условия существования сильного решения. На втором этапе находится решение системы, которое записывается в виде нечеткой матрицы. Проведено исследование влияния разброса параметров нечетких чисел на итоговый результат.
Введение
В процессе функционирования многоотраслевой экономики каждая отрасль выступает, с одной стороны, производителем некоторой продукции, а, с другой стороны, потребителем продукции, произведенной другими отраслями. При этом возникает проблема нахождения объема производства каждой из отраслей, достаточного для выполнения производственного задания. Для ее решения предложена математическая модель, сводящая проблему к решению системы линейных алгебраических уравнений [Бортаковский, 2015]. При этом считается, что все параметры модели известны точно. Однако в практике экономических расчетов обычно имеется неопределенность параметров, описываемая интервалами возможных значений. Кроме того, численному значению из интервала может быть поставлена в соответствие степень уверенности, которая в теории нечетких множеств задается так называемыми функциями принадлежности [Dubois, 1980; Matinfar, 2008; Nasseri, 2008]. Одним из возможных типов функций принадлежности являются треугольные, которые задают треугольные числа.
Предлагается сформировать нечеткий аналог математической модели выполнения производственного задания, в которой элементы матриц прямых затрат и вектора конечного спроса задаются треугольными числами. При этом система линейных уравнений трактуется как полностью нечеткая, решение которой ищется в классе треугольных нечетких чисел [Dubois, 1980; Matinfar, 2008]. Различные методы решения таких систем предложены в [Nasseri, 2008; Malkawi, 2014; Dehghan, 2006]. Авторами описан алгоритм решения полностью нечеткой системы уравнений, который реализован в виде программного обеспечения, эффективность которого продемонстрирована в ходе анализа нечеткой модели. В случае четкой матрицы системы, но нечеткого описания правых частей, могут быть использованы методы, описанные в [Пантелеев, 2019].
Задача описания и анализа модели выполнения производственного задания при наличии четкой информации
Рассмотрим классическую задачу анализа взаимосвязи между различными секторами экономики, производящими товары и услуги [Бортаковский, 2015]. В качестве единицы измерения объемов товаров и услуг каждого сектора выберем их стоимость. Произведенная каждой конкретной отраслью продукция разделяется на две части: промежуточную продукцию, которая продается отрасли-покупателю, использующей ее в дальнейшем для производства других видов продукции; конечную продукцию, которая продается покупателю, не использующему ее в сфере производства. В соответствии с этим делением спрос также подразделяется на промежуточный и конечный. Конечный спрос определяется личным потреблением, экспортом и т.д. Он оценивается в результате исследования рынка. Конечный спрос определяет объем конечной продукции во всех секторах. Регулирующий орган выдает производственное задание по каждому сектору.
Требуется найти, сколько продукции следует произвести в каждом секторе экономики, чтобы выполнить производственное задание.


Задача описания и анализа модели выполнения производственного задания при наличии нечеткой информации
На практике при задании элементов матриц, описывающих математическую модель, информация может быть размытой, т.е. представляться некоторым отрезком возможных значений. Более того, возможен случай, когда задается четкое значение и границы отрицательного и положительного изменений относительно четкого значения. В этом случае можно описать элементы матриц с помощью нечетких чисел и операций над ними, в частности треугольных чисел. Приведем основные определения, которые будут использоваться при составлении нечеткой математической модели выполнения производственного задания [Dubois, 1980; Matinfar, 2008].
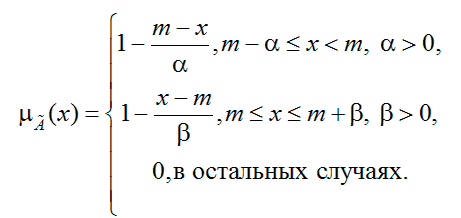
1. Треугольное нечеткое число ![]() задается функцией принадлежности (рис. 1) Число
задается функцией принадлежности (рис. 1) Число ![]() = (0,0,0) считается нулевым треугольным нечетким числом.
= (0,0,0) считается нулевым треугольным нечетким числом.
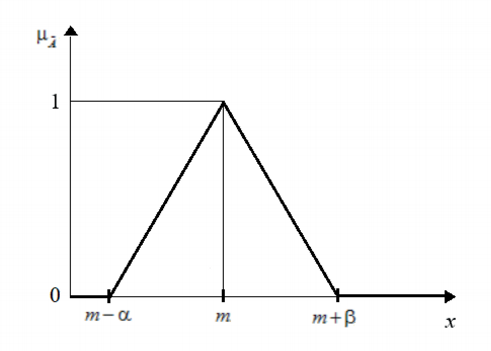
Рис. 1. Представление треугольного нечеткого числа


Методы решения полностью нечетких линейных систем


Пример анализа модели выполнения производственного задания при нечеткой информации о коэффициентах прямых затрат, конечном спросе и производственном задании



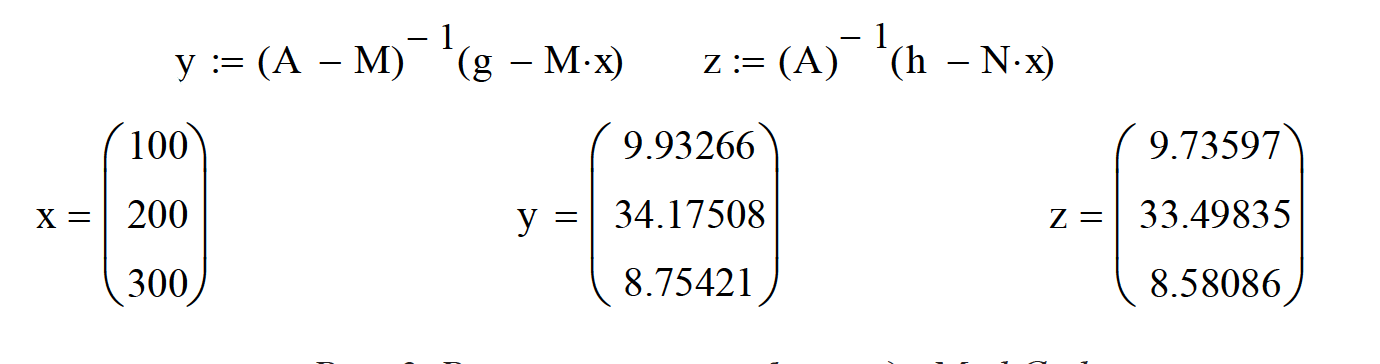
Рис. 2. Решение примера 1 в среде MathCad
Применение формул (9) и созданного программного обеспечения продемонстри- ровано на рис. 3.
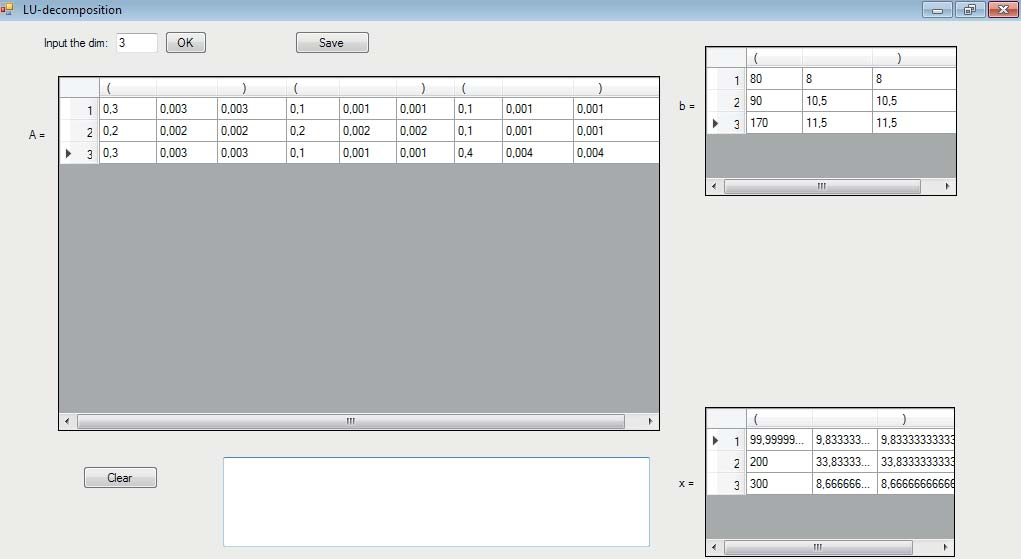
Рис. 3. Результаты расчетов в примере 1.

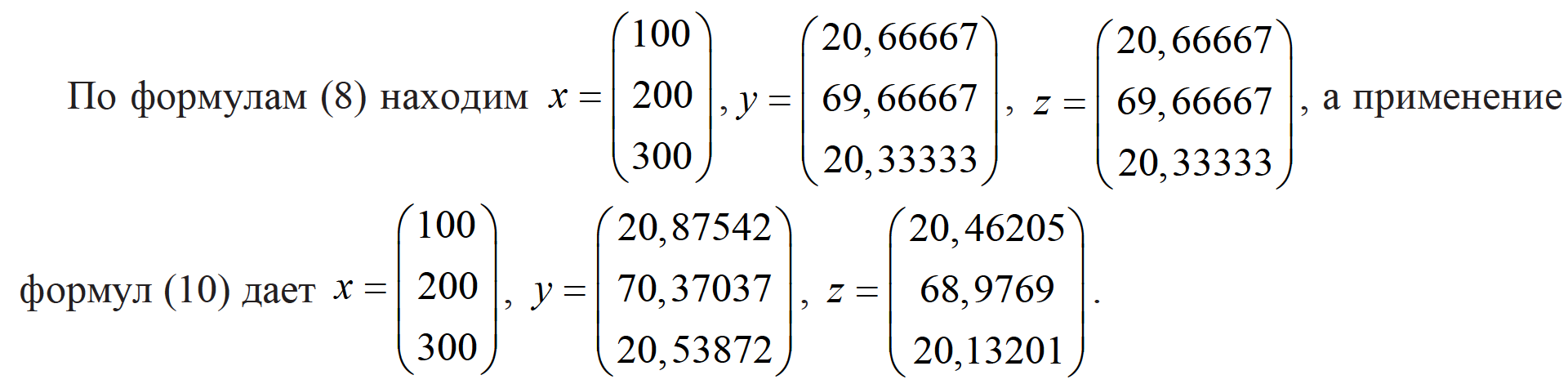
Результат применения LU-разложения показан на рис. 4.
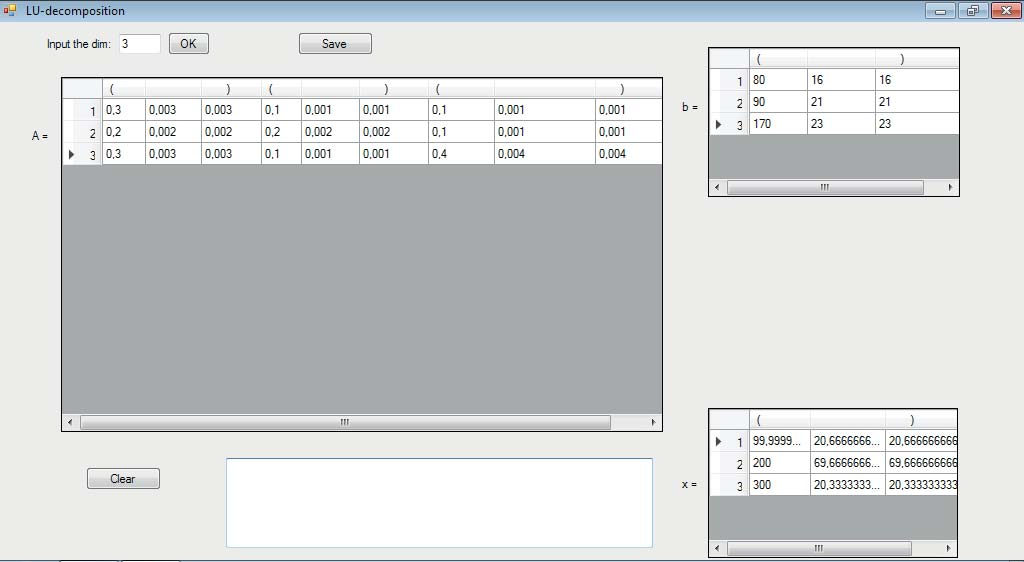
Рис. 4. Результаты расчетов в примере 2.

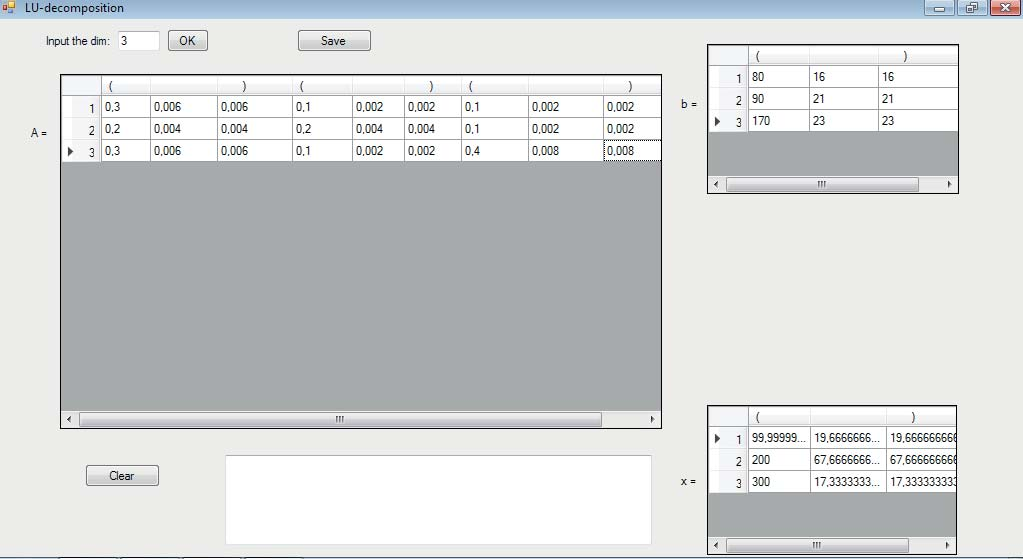
Рис. 5. Результаты расчетов в примере 3.

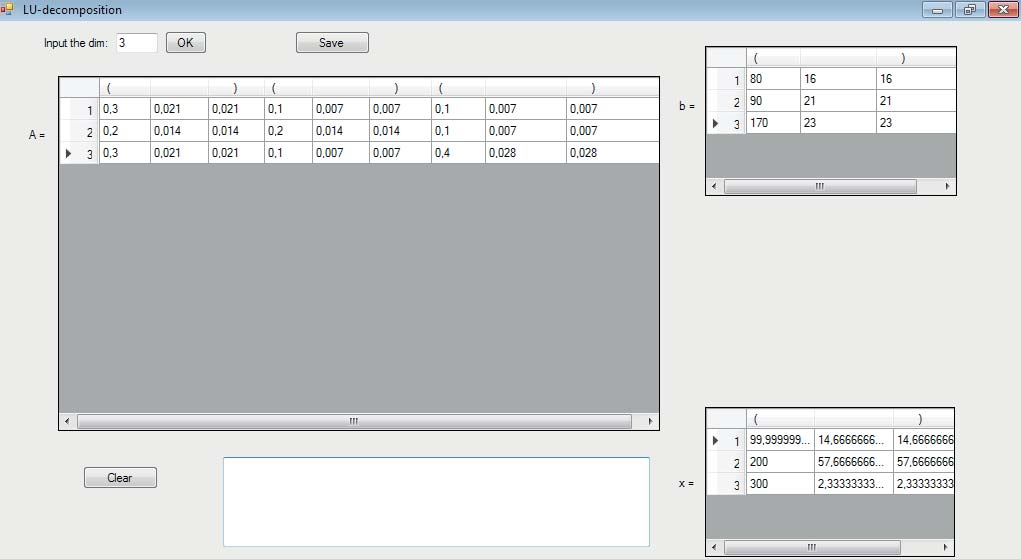
Рис. 6. Результаты расчетов в примере 4.

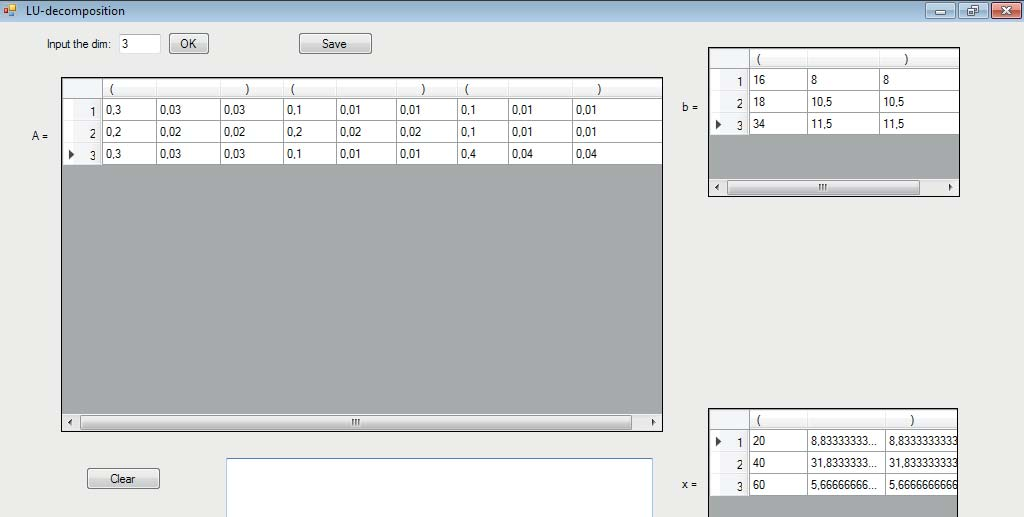
Рис. 7. Результаты расчетов в примере 5.
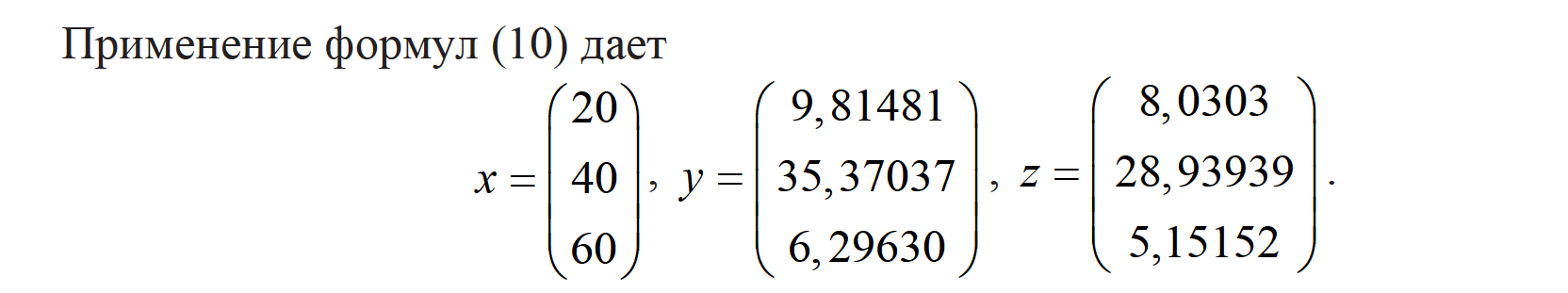
Результаты расчетов демонстрируют, что неопределенности задания элементов матриц коэффициентов прямых затрат, конечного спроса и производственного задания существенно влияют на результат. При малых разбросах значений параметров могут применяться формулы (8), при более значимых разбросах - выведенные в работе формулы (10). Существуют наборы начальных данных, при которых не существует положительное нечеткое решение полностью нечеткой линейной системы уравнений.
Заключение
Сформирована математическая модель выполнения производственного задания при нечеткой информации о коэффициентах прямых затрат, конечном спросе и производственном задании с помощью аппарата треугольных нечетких чисел и полностью нечетких линейных систем уравнений. Описаны три приближенных метода решения полностью нечеткой линейной системы. Приведены примеры анализа влияния неопределенности задания коэффициентов матрицы прямых затрат, матрицы-столбца конечного спроса, матрицы-столбца производственного задания на изменение объемов выпуска продукции в различных секторах экономики при помощи сформированной полностью нечеткой линейной модели.
Литература
- Бортаковский А.С., Пантелеев А.В. Линейная алгебра и аналитическая геометрия. Практикум. – М.: ИНФРА–М, 2015.
- Киреев В.И., Пантелеев А.В. Численные методы в примерах и задачах. – СПб.: Лань, 2015.
- Пантелеев А.В., Савельева В.С. Алгоритмическое и программное обеспечение исследования математической модели межотраслевого баланса при нечеткой информации о конечном спросе // Моделирование и анализ данных. 2019. № 3. С. 11–23.
- Dubois D., Prade H. Fuzzy sets and systems: theory and applications, Academic Press, New York, 1980.
- Matinfar M., Nasseri S.H., Sohrabi M. Solving fuzzy linear system of equations by using Housholder decomposition method // Applied Mathematical Sciences. 2008. V.51. P. 2569–2575.
- Nasseri S.H., Sohrabi M., Ardil E. Solving fully fuzzy linear systems by use of a certain decomposition of the coeffi cient matrix // World Academy of Science, Engineering and Technology. 2008. V.19. P. 784–786.
- Malkawi G., Ahmad N., Ibrahim H. Solving Fully Fuzzy Linear System with the Necessary and Suffi cient Condition to have a Positive Solution //Appl. Math. Inf. Sci. 2014. V. 8, No. 3, P. 1003–1019.
- Dehghan M., Hashemi B., Ghatee M. Computational Methods for Solving Fully Fuzzy Linear Systems// Alied Mathematics and Computation. 2006. V. 179. P. 328–343.
Информация об авторах
Метрики
Просмотров
Всего: 645
В прошлом месяце: 13
В текущем месяце: 0
Скачиваний
Всего: 178
В прошлом месяце: 2
В текущем месяце: 0