Моделирование и анализ данных
2019. Том 9. № 3. С. 43–57
ISSN: 2219-3758 / 2311-9454 (online)
Разработка и применение многокритериального метода фейерверков в задаче стабилизации движения искусственного спутника по круговой орбите
Аннотация
Общая информация
Ключевые слова: Многокритериальная оптимизация, метаэвристические методы, недоминируемая сортировка, оптимальность по Парето, теория оптимального управления
Рубрика издания: Теория управления
Тип материала: научная статья
Для цитаты: Пантелеев А.В., Крючков А.Ю. Разработка и применение многокритериального метода фейерверков в задаче стабилизации движения искусственного спутника по круговой орбите // Моделирование и анализ данных. 2019. Том 9. № 3. С. 43–57.
Полный текст
В статье рассматривается применение метаэвристичеких методов условной глобальной оптимизации к нахождению эффективного программного управления в задаче стабилизации спутника на круговой орбите. Изучается задача с фиксированным правым концом и известным конечным временем, где управление ищется в классе кусочно-постоянных функций, удовлетворяющих ограничениям. Управление должно одновременно минимизировать значения квадратичного критерия и критерия, описывающего расход топлива. Под решением многокритериальной задачи понимается множество решений, оптимальных по Парето. Предлагается численный метод многокритериальной оптимизации для приближенного решения задачи на основе генерации допустимых решений методом фейерверков и процедуры недоминируемой сортировки. На первом этапе решается оптимизационная задача относительно каждого из критериев, а для удовлетворения терминальных ограничений подбираются значения параметров штрафа. При этом применяются известные метаэвристические методы: взрыва гранат, большого взрыва-большого сжатия, фейерверков. На втором этапе найденные значения параметров используются для формулировки многокритериальной задачи оптимизации, которая решается с помощью предложенной авторами модификации метода фейерверков.
ВВЕДЕНИЕ
В современном мире проектирование новых технических систем становится все более сложным. Требования к системам в различных областях растет, поэтому приходится учитывать множество различных факторов [14, 15]. Эти факторы могут отражать противоположные требования, которые приводят к конфликту целей. Важно найти компромисс между противоречащими друг другу требованиями. Как правило, для выбора оптимальных параметров формулируется задача оптимизации. Сравнение решений происходит на основе значений критериев, каждый критерий должен соответствовать определенному фактору и отражать степень влияния решения на этот фактор.
Для соблюдения компромисса между критериями под оптимальным решением понимается решение, оптимальное по Парето [Подиновский, 1982]. Нахождение таких решений может быть важным шагом как в дальнейшем процессе принятия решений, так и в получении всех возможных конфигураций какой-то системы, которые не позволяют улучшить значение по одному критерию без ухудшения значений по другим. Поэтому разработка новых эффективных методов для решения задач многокритериальной оптимизации является важным направлением исследований.
На данный момент продолжается разработка различных численных методов для решения задач многокритериальной оптимизации. Здесь можно выделить два направления развития: первое направление основано на аппроксимации оболочки Эджворта-Парето [Березкин, 2014], а второе на аппроксимацию границы Парето [13, 16].
Появление новых численных методов [3, 8, 9] для решения многокритериальных задач и их программных реализаций позволяет рассматривать новые постановки задачи, которые раньше было сложно решать даже численно.
Например, в теории управления можно рассматривать задачи нахождения управления, которое минимизирует сразу несколько критериев. Одним из подходов к решению таких задач может быть составление свертки критериев. В этом случае могут существовать решения, оптимальные по Парето, которые невозможно найти (nonsupported solutions) [Talbi, 2009]. Представляет интерес найти численное решение задачи без составления свертки критериев. Многокритериальная задач оптимального управления была рассмотрена в работе [Прасад, 1975], но основывается на идеях из теории игр.
В статье рассматривается подход на основе аппроксимации границы Парето. Предлагается модификация метода фейерверков однокритериальной оптимизации [Tan, 2010], применимая для решения задач многокритериальной оптимизации. Метод относится к метаэвристиче- ским алгоритмам, которые оказались эффективными при решении различных прикладных задач [Glover, 2003].
1. ПОСТАНОВКА ЗАДАЧИ
Рассмотрим задачу об устойчивости стационарного движения спутника относительно оси, ортогональной к плоскости ее круговой орбиты [Бабаджанянц, 2003]. Если пренебрегать гравитационными моментами по сравнению с управляющими моментами, то уравнения Эйлера заменяются следующими:


2. СТРАТЕГИЯ ПОИСКА РЕШЕНИЯ
Исходная задача теории управления свелась к задаче многокритериальной оптимизации. Далее рассматривается алгоритм решения таких задач в общей постановке. Рассматривается задача многокритериальной оптимизации с параллелепипедными ограничениями. Предполагается, что все критерии имеют одинаковую важность и уменьшение значения одного критерия при фиксированных значениях остальных критериев более предпочтительно:

Требуется найти аппроксимацию множества допустимых решений, оптимальных по Парето. Для того чтобы дать определение решений, оптимальных по Парето, необходимо ввести несколько дополнительных определений.
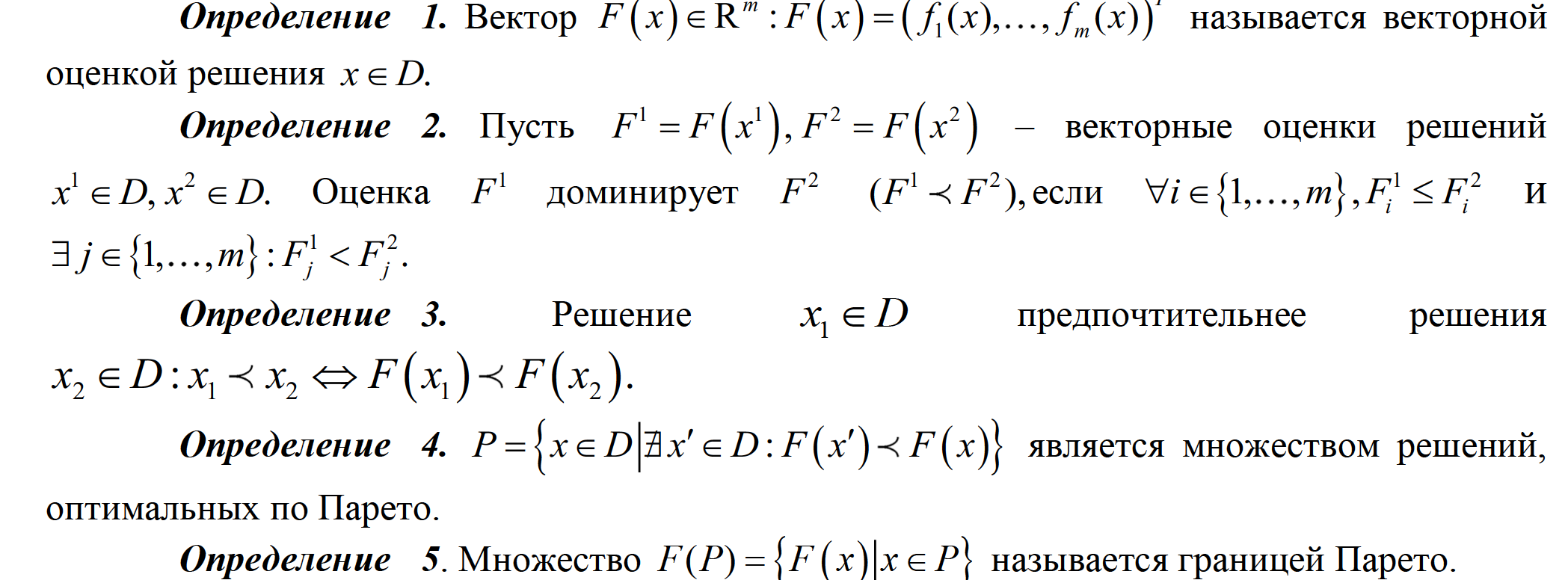
Приближенным решением задачи будет конечное множество решений, в котором каждый элемент достаточно близко расположен к какому-то элементу из P .
Для решения задачи будет использоваться модификация метода фейерверков [Tan, 2010], основанного на имитации процесса, происходящий во время фейерверка (салюта). Фейерверк сопровождается облаком светящихся осколков, заполняющих окрестность взорвавшегося заряда. В задачах оптимизации этот процесс ассоциируется с процедурой локального поиска.
Каждый залп салюта определяет переход от одной итерации поиска к другой (от одного поколения решений к другому). Сначала для реализации первого залпа определяются NP точек (решений) в множестве допустимых решений. В этих точках происходит взрыв, генерирующий определенное количество осколков, разлетающихся от точек взрыва в окрестности некоторого радиуса, определяемого для каждой точки в отдельности.

Другими словами, недоминируемая сортировка представляет собой повторяющуюся процедуру выделения предпочтительных решений. На первом шаге выбираются предпочтительные решения из I . Далее эти предпочтительные решения удаляются из I , и процедура повторяется к оставшейся части.
Среди решений, соответствующих точкам взрыва и полученным осколкам, выбираются решения с недоминируемыми векторными оценками (множество Q1 ). Остальные решения выбираются из оставшихся случайным образом с вероятностью, определяемой расстоянием в пространстве критериев до других точек (чем больше суммарное расстояние, тем больше вероятность выбора), либо выбираются решения из множествQ1,Q2,...,QR, пока количество выбранных решений не будет равно NP . Если в каком-то подмножестве решений больше, чем необходимо взять, то часть решений выбирается случайным образом на основе расстояний до других решений в пространстве критериев.

3. АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ



4. ЧИСЛЕННЫЙ ЭКСПЕРИМЕНТ

Таблица 1. Параметры для метода «большого взрыва-большого сжатия»
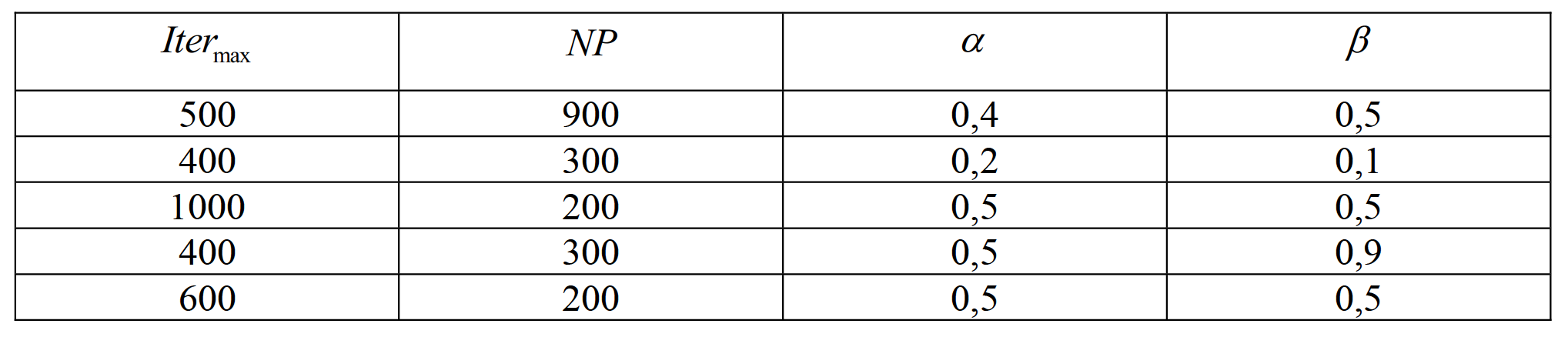
Таблица 2. Результат решения методом «большого взрыва-большого сжатия»

Таблица 3. Параметры для метода «фейерверков»
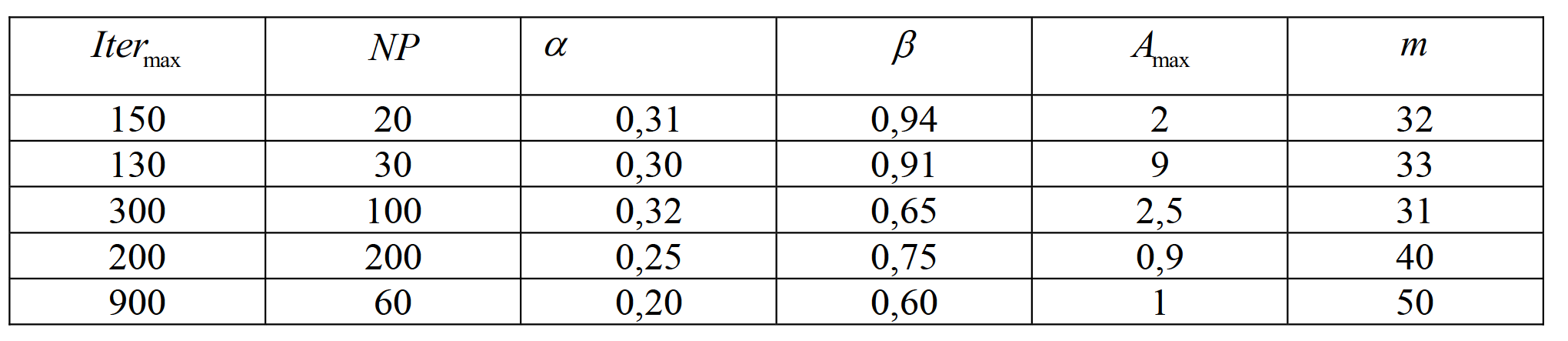
Таблица 4. Результат решения методом «фейерверков»
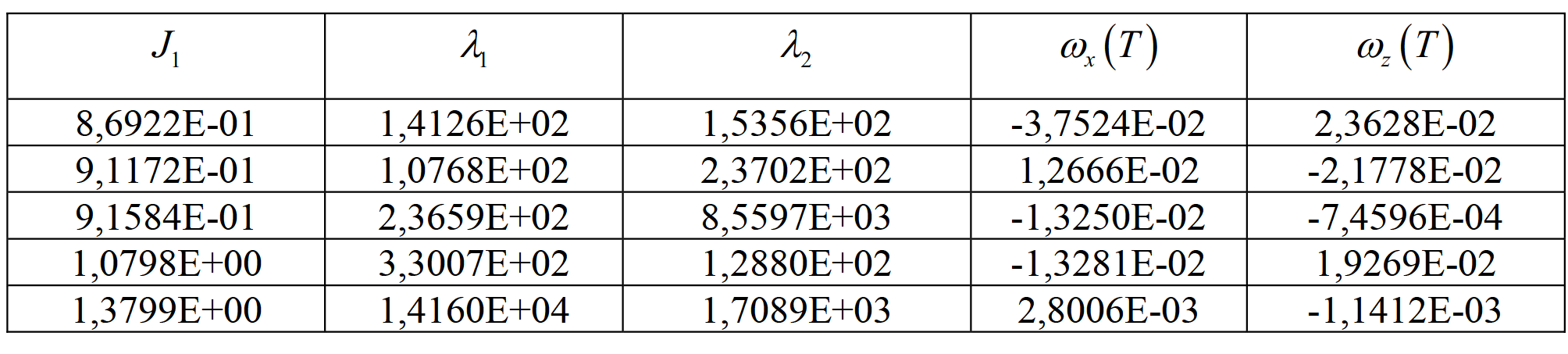
Таблица 5. Параметры для метода «взрыва гранат»
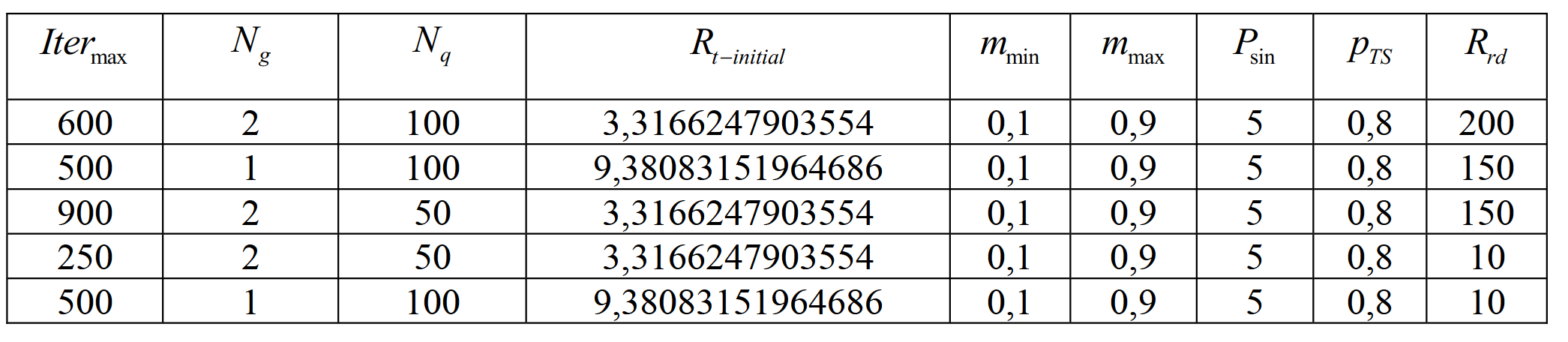
Таблица 6. Результат решения методом «взрыва гранат»
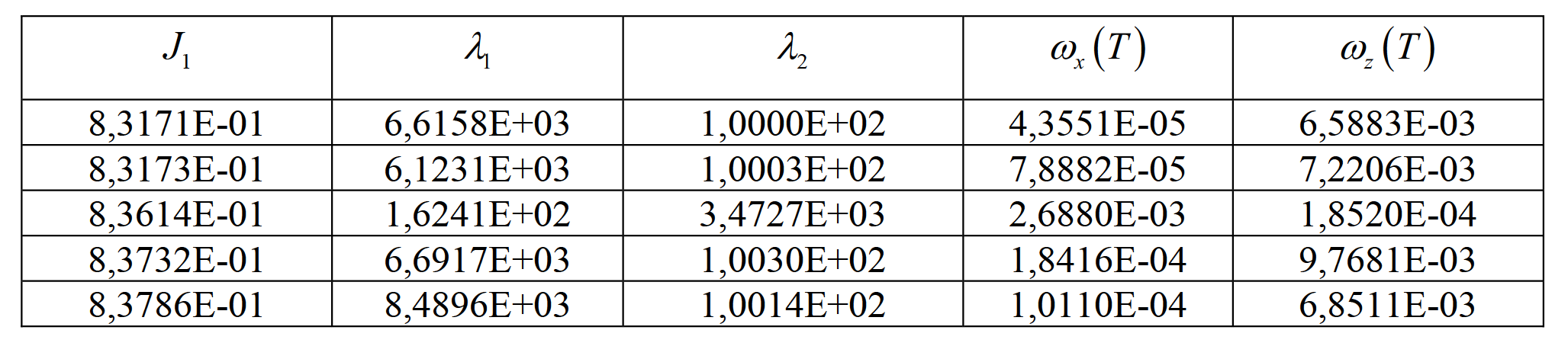
Результаты решения задачи оптимизации критерия J2 приведены в табл. 0-9. Параметры методов такие же, как и для первого критерия.
Таблица 7. Результат решения методом «большого взрыва-большого сжатия»
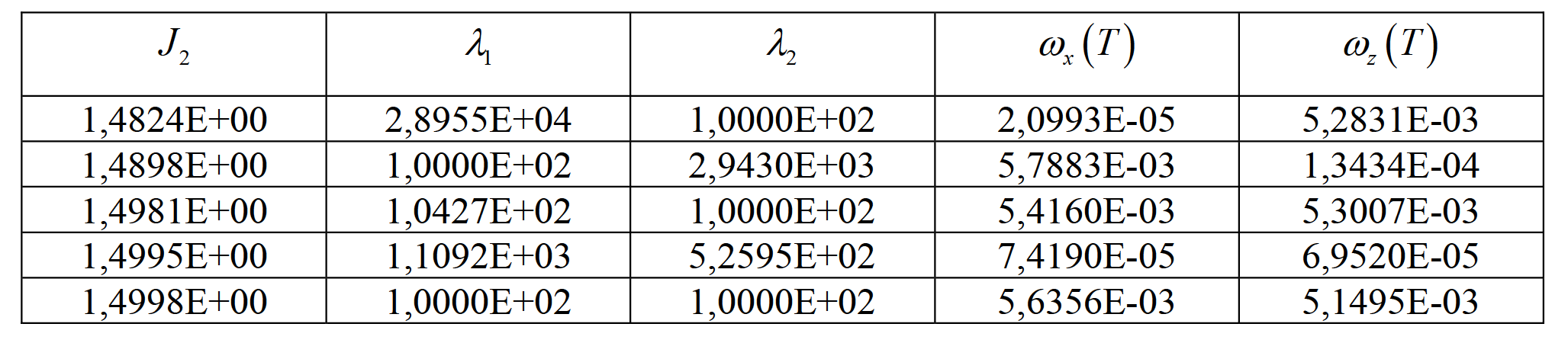
Таблица 8. Результат решения методом «фейерверков»
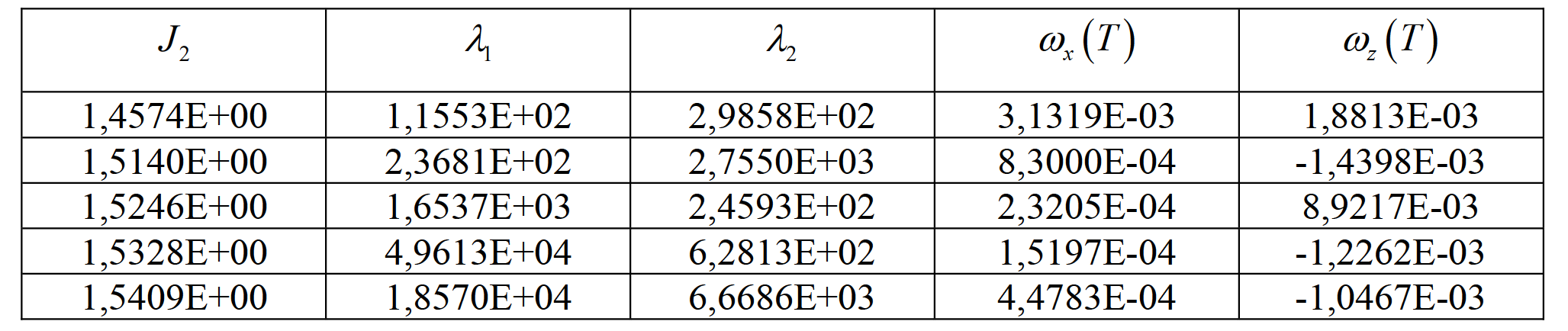
Таблица 9. Результат решения методом «взрыва гранат»
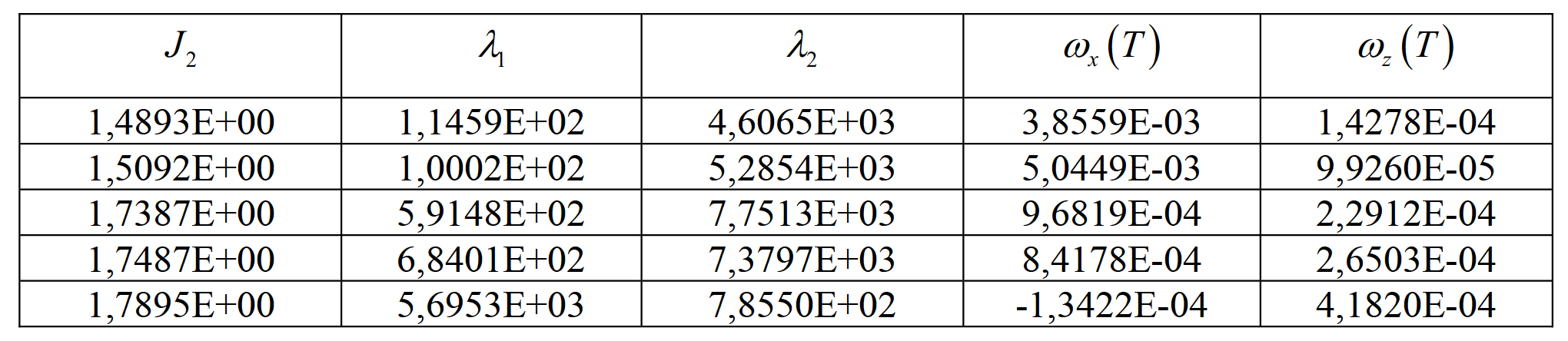

Таблица 10. Значения управления для критерия J

Таблица 11. Значения управления для критерия J2
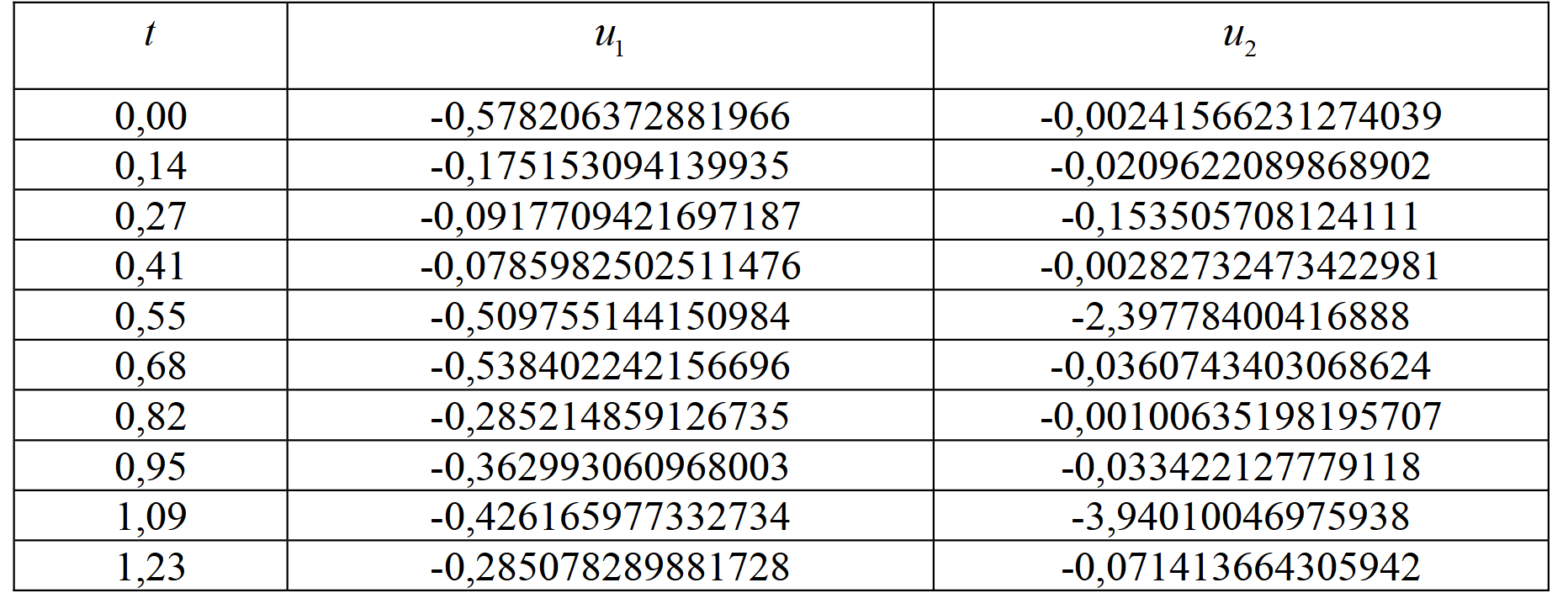
Для решения многокритериальной задачи были выбраны следующие параметры, ко- торые представлены в табл. 0.
Таблица 12. Параметры для модифицированного метода «фейерверков»
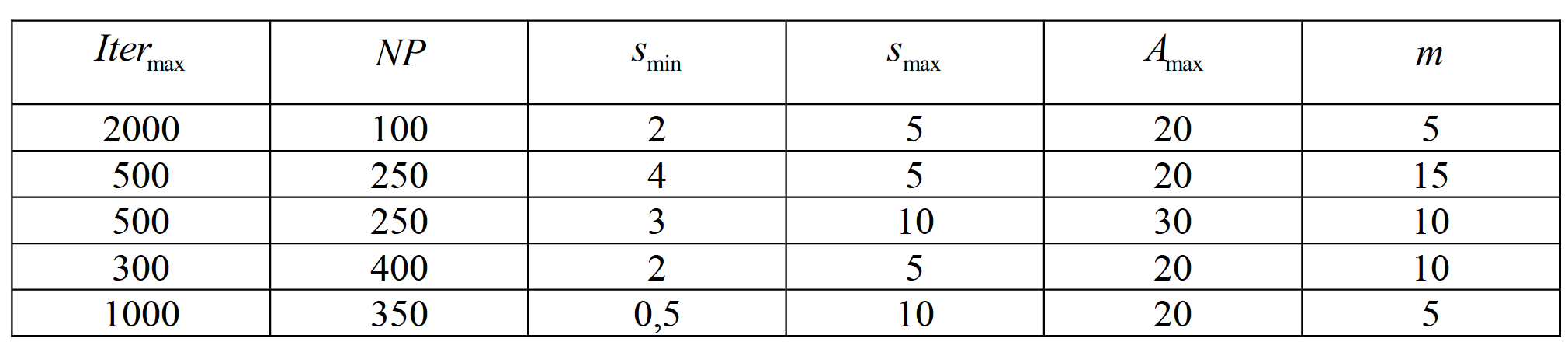
Для каждого набора параметров задача решалась 10 раз. На рис. изображена при- ближённая граница Парето (на горизонтальной оси представлены значения модифицирован- ного критерия J1, на вертикальной оси значения модифицированного критерия J2 ).

Рисунок 1. Приближённая граница Парето.
В табл. 0 представлены значения критериев для найденных решений и состояния си- стемы в конечный момент времени, соответствующие выделенной области на рис. выше.
Таблица 13. Значения критериев и конечные состояния


В табл. А приложения представлены значения управления. Пустые строки в таблице отделяют значения управления для разных решений.
ЗАКЛЮЧЕНИЕ
В статье предложена идея численного решения многокритериальных задач нахождения программного управления. Рассмотрена задача стабилизации спутника, в которой управление в силу линейности системы искалось в классе кусочно-постоянных функций. Исходная задача сведена к задаче параметрической оптимизации, в которой решением являлся вектор из действительных чисел.
Для решения многокритериальной задачи нахождения управления была сформирована новая задача с модифицированными исходными критериями, в которые добавлены штрафные функции, параметры которых найдены при решении оптимизационных задач для каждого критерия. Предложен алгоритм решения многокритериальных задач оптимизации. Алгоритм является численным и не гарантирует нахождения точного решения. Из-за этого найденное управление является лишь субоптимальным. В прикладных задачах, где нахождение точного аналитического решения невозможно, найденные решения могут считаться приемлемыми в зависимости от требований к системе.
Литература
- Березкин В.Е., Лотов А.В., Лотова Е.А. Изучение гибридных методов аппроксимации оболочки Эджворта–Парето в нелинейных задачах многокритериальной оптимизации // Журнал вычислительной математики и математической физики. 2014. № 6 (54). C. 905–918. doi: 10.7868/S0044466914060039
- Пантелеев А.В., Крючков А.Ю. Метаэвристические методы оптимизации в задачах оценки параметров динамических систем // Научный вестник МГТУ ГА. 2017. № 20(2). С. 37-45. doi: 10.26467/2079-0619-2017-20-2-37-45
- Евтушенко Ю.Г., Посыпкин М.А. Метод неравномерных покрытий для решения задач многокритериальной оптимизации с гарантированной точностью // Журнал вычисли-тельной математики и математической физики. 2013. № 2 (53). C. 144–157. doi: 10.7868/S0044466913020087
- Прасад У.К., Сарма И.Д. Многокритериальные задачи оптимального управления: игро-вое кооперативное решение по Нэшу-Харсани // Автомат. и телемех. 1975. № 6 (36). C. 95–105.
- Подиновский В.В., Ногин В.Д. Парето-оптимальные решения многокритериальных за-дач. Москва: Наука, 1982. 256 c.
- Бабаджанянц Л.К., Потоцкая И.Ю. Управление по критерию расхода в механических системах, Санкт - Петербург:, 2003. 137 c.
- Buzdalov M., Shalyto A. A Provably Asymptotically Fast Version of the Generalized Jensen Algorithm for Non-dominated Sorting // Parallel Problem Solving from Nature - PPSN XIII: 13th International Conference, Ljubljana, Slovenia, September 13-17, 2014. Proceedings, Cham: Springer International Publishing, 2014, pp. 528–537. doi: 10.1007/978-3-319-10762-2_52
- Deb K., Jain H. An Evolutionary Many-Objective Optimization Algorithm Using Reference-Point-Based Nondominated Sorting Approach, Part I: Solving Problems With Box Con-straints // IEEE Transactions on Evolutionary Computation. 2014. № 4 (18). C. 577–601. doi: 10.1109/TEVC.2013.2281535
- Jamwal P.K., Abdikenov B., Hussain S. Evolutionary Optimization Using Equitable Fuzzy Sorting Genetic Algorithm (EFSGA) // IEEE Access. 2019. (7). C. 8111–8126. doi: 10.1109/TEVC.2013.2281535
- Tan Y., Zhu Y. Fireworks Algorithm for Optimization, Berlin, Heidelberg: Springer Berlin Heidelberg, 2010, pp. 355–364. doi: 10.1007/978-3-642-13495-1_44.
- Fortin F.-A., Grenier S., Parizeau M. Generalizing the improved run-time complexity algo-rithm for non-dominated sorting // Proc. 15th Annu. Conf. Genet. Evol. Comput. 2013, pp. 615–622. doi: 10.1145/2463372.2463454
- Glover F., Kochenberger G.A. (eds.). Handbook of Metaheuristics. Boston, MA: Kluwer Ac-ademic Publishers, 2003.
- Talbi E.G. Metaheuristics: From Design to Implementation / E.G. Talbi, Hoboken: John Wiley & Sons, Inc., 2009.
- Arias-Montano, Alfredo, A. Coello Coello, Carlos Mezura-Montes, Efrén. Multiobjective Evolutionary Algorithms in Aeronautical and Aerospace Engineering// IEEE Transactions on Evolutionary Computation, 2012,16, pp. 662-694. doi: 10.1109/TEVC.2011.2169968.
- Rangaiah G.P. Multi-Objective Optimization. G.P. Rangaiah, 2nd-е., World Scientific, 2017. doi: 10.1142/10240
Информация об авторах
Метрики
Просмотров
Всего: 594
В прошлом месяце: 5
В текущем месяце: 4
Скачиваний
Всего: 268
В прошлом месяце: 2
В текущем месяце: 1