Методы определения среднего в системах контроля процесса обучения

В статье приводятся данные о проведенном исследовании на тему целесообразности использования альтернативного метода определения среднего балла в процессе электронного тестирования обучающихся. Составляется экспериментальный процесс на основе которого проверятся адекватность оценки среднего при помощи медианы вместо традиционного метода математического ожидания.

В статье приводятся данные о проведенном исследовании на тему целесообразности использования альтернативного метода определения среднего балла в процессе электронного тестирования обучающихся. Составляется экспериментальный процесс на основе которого проверятся адекватность оценки среднего при помощи медианы вместо традиционного метода математического ожидания.

В современных электронных системах обучения выдвигаются высокие требования к качеству полученных знаний. Дистанционное обучение ввиду отсутствия личного контакта обучаемых с преподавателями не всегда позволяет оценить качество полученных знаний при обычном просмотре результатов тестирования. Вследствие вышесказанного необходимо подобрать метод оценки результатов тестирования учебных групп. В ходе данного исследования процесс обучения предполагается рассматривать как некий производственный процесс с ожидаемым уровнем качества. Одним из наиболее часто применяемых методов контроля качества на производстве являются контрольные карты Шухарта. Карта Шухарта требует данных, получаемых выборочно из процесса через примерно равные интервалы. Интервалы могут быть заданы либо по времени (например, ежечасно), либо по количеству продукции (каждая партия). Обычно каждая подгруппа состоит из однотипных единиц продукции или услуг с одними и теми же контролируемыми показателями, и все подгруппы имеют равные объемы. Для каждой подгруппы определяют одну или несколько характеристик, таких как среднее арифметическое подгруппы и размах подгруппы R или выборочное стандартное отклонение. Карта Шухарта - это график значений определенных характеристик подгрупп в зависимости от их номеров. Она имеет центральную линию (CL), соответствующую эталонному значению характеристики. При оценке того, находится ли процесс в статистически управляемом состоянии, эталонным обычно служит среднее арифметическое рассматриваемых данных. При управлении процессом эталонным служит долговременное значение характеристики, установленное в технических условиях, или ее номинальное значение, основанное на предыдущей информации о процессе, или намеченное целевое значение характеристики продукции или услуги. Карта Шухарта имеет две статистические определяемые контрольные границы относительно центральной линии, которые называются верхней контрольной границей (UCL) и нижней контрольной границей (LCL) (рисунок 1).

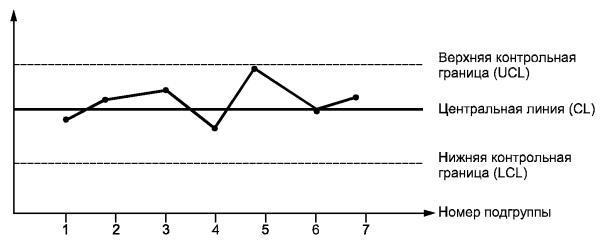
Рис. 1 Вид контрольной карты

Контрольные границы на карте Шухарта находятся на расстоянии 3s от центральной линии, где s - генеральное стандартное отклонение используемой статистики. Изменчивость внутри подгрупп является мерой случайных вариаций. Для получения оценки s вычисляют выборочное стандартное отклонение или умножают выборочный размах на соответствую- щий коэффициент. Эта мера не включает межгрупповых вариаций, а оценивает только из- менчивость внутри подгрупп. 

Границы ± 3s указывают, что около 99,7 % значений характеристики подгрупп попа- дут в эти пределы при условии, что процесс находится в статистически управляемом состоя- нии. Другими словами, есть риск, равный 0,3 % (или в среднем три на тысячу случаев), что нанесенная точка окажется вне контрольных границ, когда процесс стабилен. Употребляется слово «приблизительно», поскольку отклонения от исходных предположений, таких как вид распределения данных, будут влиять на значения вероятности.

Для процесса оценивания при помощи контрольных карт способом определения сред- него согласно стандарту, используется математическое ожидание. В данной статье проверке подвергается гипотеза, что для частного случая контроля процесса обучения более адекват- ной оценкой может выступать медиана. Математическим ожиданием М(Х) дискретной случайной величины называют сумму произведений всех возможных значений этой величины на их вероятности

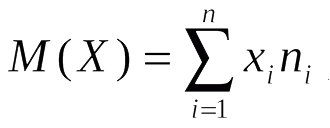
Медиана —число m, такое что Х принимает с вероятностью 1/2 как значения больше m, так и меньше m.

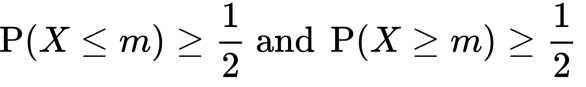
Для симуляции статистики результатов используется алгоритм генерации итогов тестирования для группы, состоящей из 30 человек. Тесты состоят из 10 вопросов, с вариантами ответа да/нет. Оценка за тест для каждого из студентов представляет собой биноминаль­ную случайную величину с n=10 и р=0.8/0.6/0.3(для обучающихся с хорошей/средней/плохой успеваемостью соответственно). Тестируемая ученая группа имеет 7 учеников с хорошей успеваемостью, 16 с средней успеваемостью и 7 учеников с плохой успеваемостью.

Биномиальной случайной величиной с параметрами n и p называется дискретная случайная величина, возможными значениями которой являются частоты появления события A в n независимых испытаниях (m=1,2,...,n), а вероятность соответствующих значений определяются по формуле Бернулли

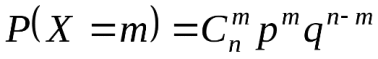
Динамика описываемого процесса считается соответствующей требованиям стабильности учебного процесса.

Оценка среднего балла группы определяется двумя способами: математическое ожидание (традиционный метод) и медиана (экспериментальный метод). Проверка результатов тестов проводилась каждый месяц в течение 1 года. Наиболее успешным методом оценки среднего будет считаться метод, оценки которого будут наиболее показательными (так как данный процесс является стабильным т.е. количество аномалий минимально, наиболее показательным будет метод с наименьшим количеством сбоев в учебном процессе).

Данные контрольные карты были созданы на основе 8 случайных наборов данных сгенерированных по вышеописанному алгоритму. Значения обведенные кругом являются аномалиями согласно методу анализа контрольных карт Шухарта. Слева представлены контрольные карты, полученные традиционным методом, а справа контрольные карты, полученные экспериментальным методом.

Условные обозначения:

Data-экспериментальные значения

Violation-Нарушение стабильности процесса

Center-Центральное значение

LCU/UCL- Нижняя контрольная граница/Верхняя контрольная граница

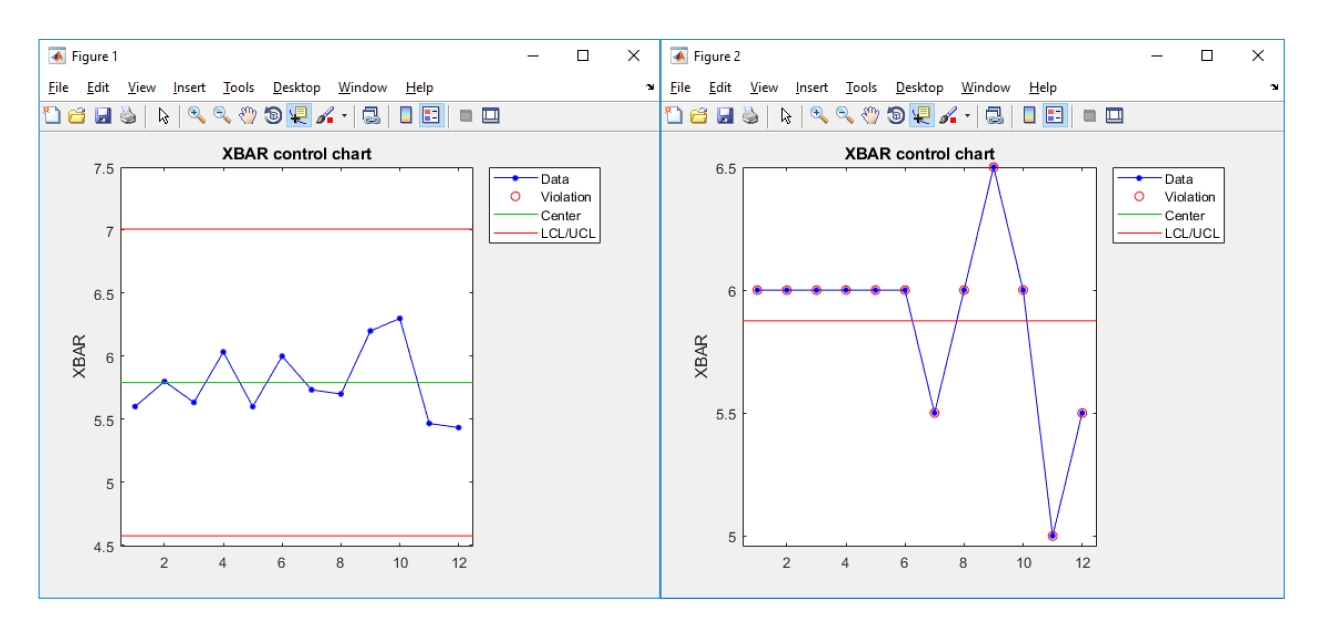
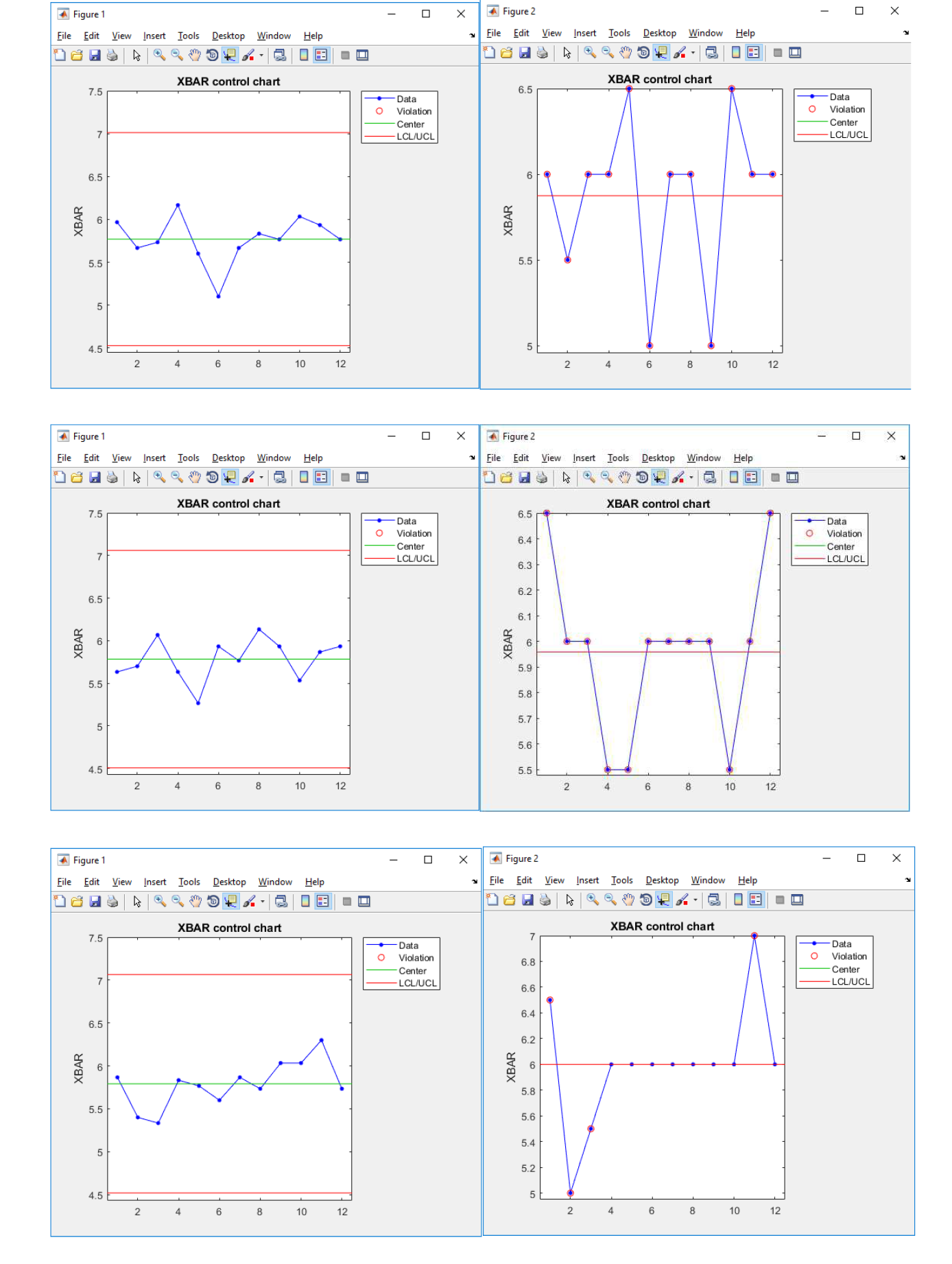
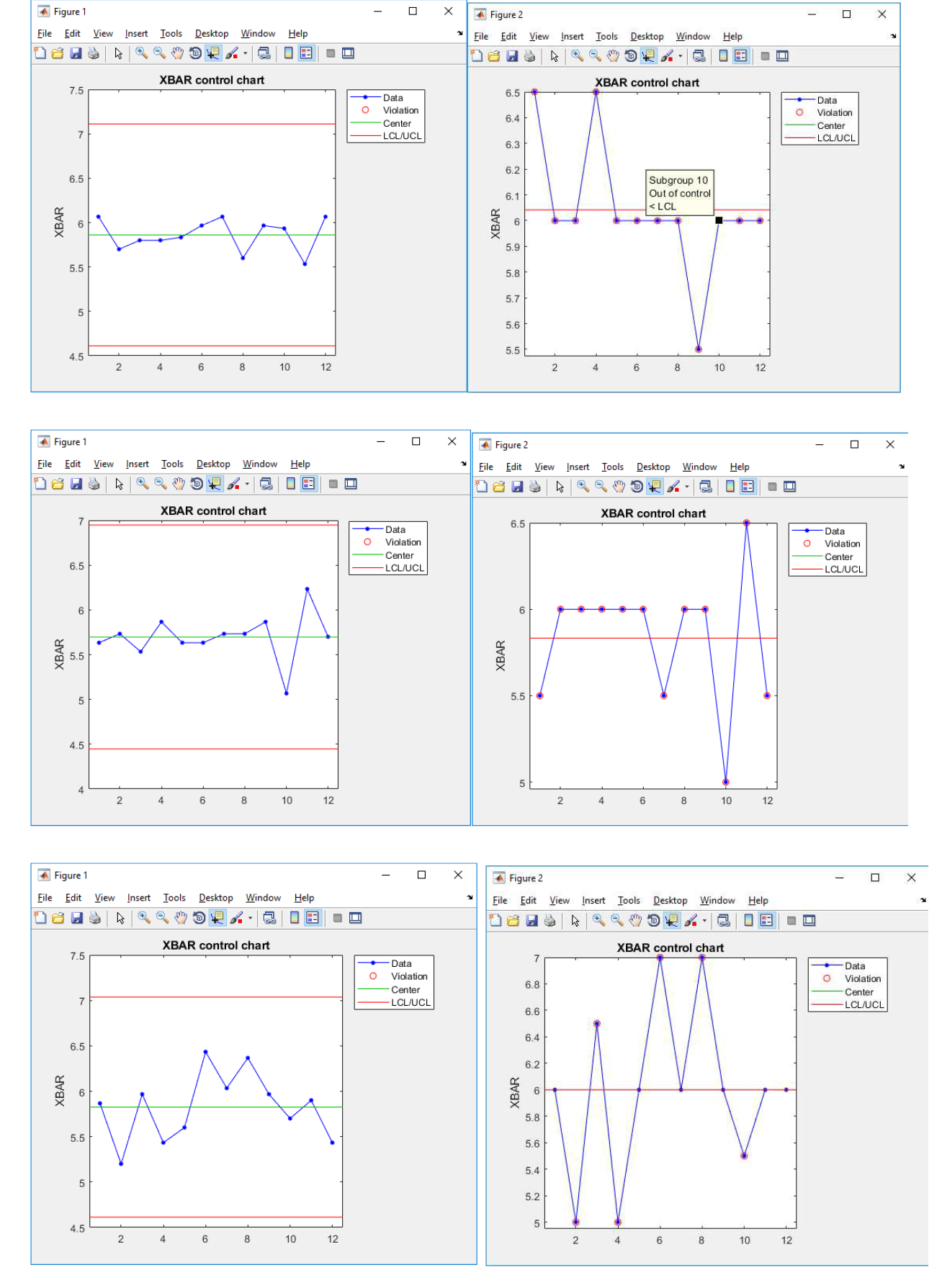
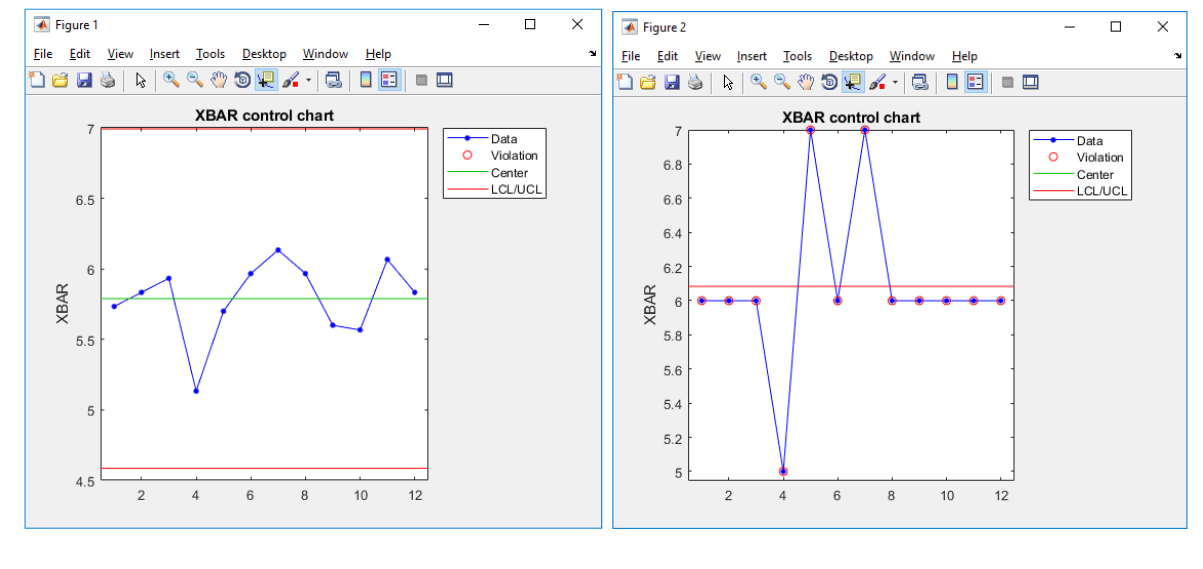
Как можно видеть экспериментальный метод выдает недопустимо большое количество оценок, говорящих о выходе учебного процесса из состояния стабильности. Множество одинаковых средних значений на разных участках временного отрезка приводит к неадекватности оценки. Это говорит о несоответствии данного способа определения среднего критериям качества.

Согласно полученным данным контроля учебного процесса метод оценки при помощи медианы показывает неинформативные результаты ввиду негибкости формулы определения медианы для набора дискретных значений, ведущих к интерпретации результатов тестирования как аномалий на заведомо достаточно стабильном наборе значений отвечающим стандартам качества процесса обучения. Математическое ожидание, используемое в данном исследовании как эталонное значение, не имеет данного недостатка, ввиду чего замена его медианой для данного частного случая использования контрольных карт Шухарта не является целесообразной.

 

1. Нельсон Л.С. Контрольные карты Шухарта - Тесты на особые случаи//Журнал «Технологии качества», 16, № 4, октябрь 1984, - с. 237 - 239
2. Шухарт У.А. Экономический контроль качества произведенного продукта // Вэн Ноустренд К., Нью-Йорк, - 1931. - 50 с.
3. https://studfiles.net/preview/5593843/
4. ИСО 7966-93* Приемочные контрольные карты
5. ГОСТ Р 50779.40-96 Статистические методы. Контрольные карты. Общее руководство и введение