Моделирование и анализ данных
2017. Том 7. № 1. С. 42–53
ISSN: 2219-3758 / 2311-9454 (online)
Из опыта работы в области тифлопедагогики
Аннотация
Общая информация
Ключевые слова: тифлопедагогика, методика преподавания математики, компьютерная графика, высшее образование
Рубрика издания: Анализ данных
Тип материала: обзорная статья
Для цитаты: Степанов М.Е. Из опыта работы в области тифлопедагогики // Моделирование и анализ данных. 2017. Том 7. № 1. С. 42–53.
Полный текст
1. ВВЕДЕНИЕ
Одним из важных направлений деятельности факультета информационных технологий Московского государственного психолого-педагогического университета является работа с инвалидами, в том числе обучение студентов с дефектами зрения. Кроме того, на факультете под руководством декана Льва Семёновича Куравского ведётся интенсивная научная работа, направленная на реализацию ряда проектов, связанных с созданием автоматизированных технических комплексов, позволяющих лицам с дефектами зрения осуществлять действия, непосредственно им недоступные, в частности ориентироваться на местности. Следует также отметить, что на факультете имеется учебно-производственная лаборатория технических и программных средств обучения студентов с нарушением зрения, которой руководит Владимир Вячеславович Соколов.
В то же время, практически каждому преподавателю факультета приходится непосредственно заниматься обучением инвалидов, в том числе и по зрению (см. например [И. М. Нуркаева, 2009]). Естественно, что при этом ему приходится, так или иначе, решать ряд проблем, относящихся к сфере тифлопедагогики. При этом, по вполне объяснимым причинам, некоторые приёмы и методы, которые возникают в работе преподавателя, остаются его личными наработками и не могут быть включены в общий и без того насыщенный план работы факультета.
Именно в такой ситуации находится автор данной статьи. Не являясь специалистом в области тифлопедагогики, автор невольно сталкивался с соответствующими проблемами. Более того, возникший при этом круг вопросов его заинтересовал. В данной статье рассказывается о попытках решить некоторые из возникших проблем. Автор надеется, что его соображения представят интерес, как для тифлопедагогов, так и для таких же, как он, педагогов
общего профиля, работающих со студентами, имеющими дефекты зрения. При этом автор не претендует на сколько-нибудь систематические и продвинутые результаты.
Что же касается тематики затрагиваемых ниже вопросов, она естественным образом вытекает из самого факта общения преподавателя со студентами, имеющими дефекты зрения. Поскольку в настоящее время всё большую роль в образовании играют компьютерные технологии, регулярно создаются программные средства, направленные на приобщение соответствующей категории учащихся к компьютеру. Важную роль при этом играют программы, озвучивающие электронные тексты. Их современный уровень можно считать вполне приемлемым. Однако озвучивание формул пока не производится. Кроме того, постоянной проблемой остаётся доведение до сознания студента образов, непосредственно связанных со зрительным восприятием, таких как чертежи, схемы, изображения геометрических объектов и т. д.
Именно вопросами этого характера и занимался автор данной статьи. Особую роль сыграли при этом научные интересы автора. Речь идёт о компьютерной геометрии - разделе науки, находящемся на границе математики и информатики и направленном на создание изображений математических объектов [2, 3]. В том числе и по этой причине автор стремился перекинуть мостик от упомянутой категории студентов к компьютерной графике. Результатом стал ряд дипломных работ, защищённых студентами факультета и направленных на приобщение слабовидящих к графике. В данной статье, в частности, даётся обзор этих работ. Но всё же хотелось бы начать с экзотического и даже наивного проекта, который возник у автора на первых этапах работы на факультете.
2. ЭКРАН АЛЕКСЕЕВА И ТИФЛОПЕДАГОГИКА
Русский художник, иллюстратор и мультипликатор Александр Александрович Алексеев (1901, Казань - 1982, Париж) в 1931 году изобрёл игольчатый экран (или экран Алексеева), а в 1935 году запатентовал его. Суть изобретения такова. Толстую прямоугольную пластину просверливают, покрывая решёткой из многочисленных отверстий. В отверстия вставляют стержни (иглы), перпендикулярные пластине, которые могут свободно скользить в отверстиях. Выдвинув их по одну сторону пластины и наложив на стержни, например, ладонь, можно получить стилизованное изображение ладони с другой стороны.
С помощью своего экрана Алексеев создавал анимационные фильмы, обладающие особой выразительностью. Он оказал влияние в частности на Юрия Норштейна. Я же узнал об Алексееве и его экране, посмотрев телепередачу на канале «Культура». Изобретение понравилось и запало в память.

Начав работать в 2004 году на факультете информационных технологий, я столкнулся необходимостью объяснять студентам с дефектами зрения, какова форма графиков и поверхностей. Тут и вспомнился игольчатый экран.
Именно такое устройство могло принести пользу, позволяя изучать кривые и поверхности с помощью осязания. Но иглы нужно было уметь закреплять в определённом положении. Первоначально я решил их заменить длинными винтами. Я даже сделал весьма неуклюжий, условно говоря, эскиз «одномерного экрана», предназначенного для демонстрации формы графиков. Его вид сбоку и снизу показан на рисунке.

В дальнейшем я продумал конструкцию более детально. Её основой должны были стать одиночные блоки, конструкцию которых можно описать так: трубка со скользящим в ней стержнем и фиксатор положения стержня.
Блоки могут крепиться на специальном прямоугольном основании n×m, подобном ситу (если m = 1, будем называть экран одномерным). Прикрепляемый к основанию блок связан с одним из отверстий на основании. Стержень получает возможность проходить через это отверстие перпендикулярно основанию. В результате появляется возможность «заметать» концами стержней плоские кривые (они требуют всего лишь одномерного экрана), пространственные кривые и поверхности.
Поскольку создание прибора, годного для практического использования, требовало значительного времени и соответствующих трудовых навыков, да и положительный результат был не гарантирован, работа над устройством была прекращена. Однако его исходная идея дала толчок ряду разработок, направленных на приобщение незрячих пользователей к компьютерной графике.
В настоящее время появились компьютерные формовочные устройства, предназначенные в частности для печати. Несомненно, что скоро будут созданы объекты, имеющие переменную управляемую форму. Но видимо, не следует списывать со счетов и управляемый компьютером экран Алексеева. В конце концов, электронное табло - всего лишь управляемая вычислительным устройством груда лампочек. Управление грудой стержней, конечно, несколько сложнее, но принципиальных отличий от табло нет.
3. СЛОВЕСНОЕ ОПИСАНИЕ ФОРМУЛ И РИСУНКОВ
Одновременно с идеями, связанными с экраном Алексеева, рассматривались и более простые пути передачи студентам с дефектами зрения пространственных образов и формул. Одним из естественных и возникающих фактически стихийно способов такой передачи является словесное описание рисунков и словесная передача формул.
Одним из первых шагов, предпринятых мной в этом направлении, было создание электронных конспектов по различным математическим темам, в которых вся информация представлена в вербальной форме. Непосредственная работа над созданием таких электронных документов потребовала определённой систематизации приёмов, которые использовались при этом.
В качестве примера электронного конспекта без формул и чертежей приведём фрагмент, посвящённый радианной мере углов, использование которой вызывает затруднения практически у всех студентов первого курса. Радианную меру как бы подавляет мера градусная, которая несравненно более привычна для выпускников средней школы.
«Важнейшей для математики мерой углов является радианная мера (от слова «радиус», указывающего на участие окружности). Для введения этой меры из вершины угла как из центра опишем окружность единичного радиуса. Теперь вращение луча, начальное и конечное положение которого как раз и образует угол, сопровождается движением точки по окружности (речь идёт о точке пересечения окружности с лучом). Теперь при вращении луча сам луч отмеряет угол, а точка на окружности - дугу.
После полного оборота луча точка пробежит по окружности расстояние равное двум пи. Если выбрать коэффициентом (на него умножаются обороты луча) для меры угла два пи, то мера угла будет совпадать с длинной дуги, пройденной точкой по окружности. Именно эта мера и называется радианной.
Если вместо единичной окружности использовать окружность радиуса эр, то при полном обороте луча точка пройдёт по окружности расстояние два пи эр, т. е. радианы умножаются на радиус. Легко понять, что если луч заметёт угол фи, то точка пройдёт по дуге расстояние, равное фи умноженное на эр. Установление простой связи между мерой угла и длиной дуги и определяет важность радианной меры углов.
Поясним, почему в математическом анализе используется именно радианная мера углов. При вычислении производной синуса используется замечательный предел отношения синуса икс к икс при икс, стремящемся к нулю. Для доказательства того факта, что данный предел равен единице, используются неравенства, снизу и сверху оценивающие площадь сектора единичной окружности, соответствующего углу фи. Эта площадь заключена между половиной синуса и половиной тангенса угла фи.
Площадь окружности равна пи эр квадрат. Она соответствует сектору в два пи радиан. Тогда сектору с углом фи соответствует площадь фи умножить на отношение пи эр квадрат к двум пи. Таким образом, площадь сектора равна половине фи эр квадрат. Отсюда следует, что для радианной меры величина угла заключена между синусом и тангенсом, а любая другая мера нарушает эти неравенства. Замечательный предел в этом случае не равнялся бы единице».
Так или иначе, в процессе создания подобных электронных документов со всё возрастающей сложностью возникли многочисленные идеи, которые частично были отражены в дипломной работе Антона Лазарева «Блочный принцип озвучивания сайтов математического содержания» (работа защищена в 2016 году). В ней формулируются принципы создания электронных пособий по математике, предназначенные для студентов с дефектами зрения.
В целом перечисленные ниже принципы образуют определённую программу создания электронных документов для студентов с дефектами зрения.
1. Один из универсальных вариантов озвучивания электронных документов состоит в переводе символьной информации в информацию вербальную вне зависимости от конкретного характера документа. Это делается с помощью таблиц, сопоставляющих наборам символов слова или звуки. Примером является «Джос». Однако это не единственный возможный подход.
2. В европейской культуре существует традиция целостного описания мира в единых логически строгих формах. В средние века её продвигал Раймонд Луллий, а в Новое время - Лейбниц. С современным состоянием проблемы можно ознакомиться по книге Умберто Эко «От дерева к лабиринту».
3. В педагогических целях подобный подход использовал Ян Амос Коменский, создавший пособие «Мир в картинках». В нём он выделил основные структуры окружающего мира и образно их описал. Эта модель мира успешно использовалась им при обучении детей.
4. Аналогичный подход можно использовать и при разработке озвученных электронных документов. На начальном этапе выделяются основные разделы математики (или другой изучаемой науки), для каждого из которых даётся максимально краткое изложение, но достаточно подробное, чтобы обеспечить общее понимание предмета без погружения в детали. В описание включаются формулы и чертежи.
5. В рамках одного электронного документа создаётся уникальное (в отличие от универсальных методов озвучивания по типу «Джоса») пособие. Оно аналогично записи концерта, спектакля, стихотворения. Такой подход должен быть оправдан высоким качеством документа.
6. Вся информация в электронном документе, в зависимости от её характера, разбивается на блоки, которые могут образовывать многоуровневую структуру. В частности блок высшего уровня можно назвать «основным текстом».
7. В сайте, разработанном в качестве конкретного примера применения соответствующих принципов, используется три вида блоков: текстовые блоки, блоки-формулы, блоки чертежи. Возможно использование и блоков иного типа, например, блоков, обеспечивающих интерактивное взаимодействие пользователя с программой.
8. При работе пользователя с электронным документом переход к очередному блоку сопровождается озвучиванием его названия, отражающего смысловую нагрузку блока. Например, блок может называться «Чертёж, разъясняющий геометрический смысл производной». Далее начинается полное озвучивание данного блока.
9. Блоки-формулы озвучиваются в соответствии с правилами их прочтения, принятыми в математике.
10. Простые формулы озвучиваются непосредственно в тексте.
11. Блоки-чертежи озвучиваются по генетическому принципу: описывается процесс постепенной прорисовки чертежа с пояснениями, обеспечивающими восприятие образа в целом.
12. Блочная структура электронных документов даёт возможность расширения уже созданных документов без кардинальной их переделки.
13. Блочная структура электронных документов даёт возможность перенесения наиболее важных блоков из одного документа в другой.
14. Блочная структура электронных документов позволяет соблюсти принцип максимальной полноты информации, обеспечивающий предоставление всех используемых понятий и терминов в рамках данного документа.
15. Блочная структура электронных документов даёт возможность создавать из отдельных документов своеобразные информационные системы.
16. При перемещении внутри электронного документа с блочной структурой возможна многоуровневая навигация, основанная на удобном описании общей блочной структуры документа. Она позволяет перемещаться от блока к блоку (например, по номерам блоков) и вызывает озвучивание блока, к которому пользователь обращается в данный момент.
17. При работе с информационными системами, включающими в себя несколько блочных документов, естественную основу общей навигационной системы составляют системы навигации каждого документа.
Необходимо признать, что разработка электронных документов, создаваемых по данной схеме, требует кропотливой работы. По этой причине проще просто озвучивать небольшие, но содержательные математические тексты. Шаги в этом направлении делались и автором этой статьи, и его студентами, которые просто записывали аудиофайлы во время лекции. Конечно, лектор заранее знал об этом и строил свою лекцию так, чтобы избегать отсылок к зрительным образам. Детально проговаривались формулы, а также проводилось вербальное описание чертежей.
Целенаправленная работа по озвучиванию материалов, помогающих в подготовке студентов с дефектами зрения к государственному экзамену, проводилась автором в 2016/2017 учебном году совместно с Анной Анатольевной Мироновой. Работа получила положительную оценку студентов по окончании государственного экзамена. Все студенты с дефектами зрения получили оценку «отлично». В определённой степени этому помогли упомянутые выше аудиоматериалы.
4. ЗВУКОВАЯ МОДЕЛЬ ФУНКЦИИ
Теперь мы переходим к вопросу о разработке инструментальных программных средств, направленных на различные способы работы пользователей с дефектами зрения с компьютерной графикой. Ниже будут изложены идеи, положенные в основу трёх дипломных работ, защищённых под моим научным руководством.
Первая работа связана с созданием звуковой модели графика функции. Речь идёт о дипломной работе Алексея Новикова «Звуковое моделирование функций одной переменной», защищенной в 2009 году. В этой работе значения той или иной функции увязывались с музыкальными звуками различной высоты.
Отметим, что в 2017 году Александр Козловский защитил диплом, в котором результаты работы Новикова перенесены на мобильный телефон.
Что касается работы Новикова, то на её основе была написана статья «Звуковое моделирование математических функций», которая по ряду причин не была напечатана. Её текст мы приводим ниже, поскольку статья даёт достаточно ясное представление о предлагаемом методе. Авторами статьи являются А. К. Новиков и М. Е. Степанов.
«Выбор темы данной статьи связан с наличием проблем, возникающих при работе на компьютере у пользователей, имеющих ограничения по зрению. Речь идёт о затруднениях, а порой и невозможности, восприятия компьютерной графики.
Доступ к текстовой информации для этой группы пользователей облегчается с помощью специальных программных средств, таких как программа экранного доступа Jaws (job access with speech), которая позволяет незрячим людям считывать текст с экрана. Специальный модуль этой программы распознаёт текст, а встроенный синтезатор озвучивает распознанную информацию. Немаловажно и то обстоятельство, что Jaws адаптирован под самую распространённую в настоящее время операционную систему Windows. Таким образом, любой текстовой электронный документ сейчас является доступным для незрячих.
Однако этого нельзя сказать о фрагментах электронных документов, содержащих графику. В качестве примера можно привести диаграммы в Excel. Именно это конкретное обстоятельство и послужило отправным пунктом нашего исследования.
Одна из тенденций современной науки связана с построением единой картины мира на основе понятий информатики и теории информации. Для учёных, избравших именно эту позицию, характерна точка зрения, согласно которой для любого реального объекта существует исчерпывающая информационная модель, в конечном счёте, представляющая собой текст. Таким образом, утверждается, что любой объект может быть исчерпывающе описан словесно.
Фактически это иное выражение убеждённости многих учёных в познаваемости мира научными методами. Не обсуждая правильность этой позиции, отметим, что не только людям искусства, но и тем, кто достаточно далёк и от науки, и от искусства, научное описание представляется сухим и обезличенным, лишённым эмоционального стержня.
Общеизвестно, что человеку свойственно эмоциональное и образное восприятие мира. Достаточно вспомнить о существовании текстов принципиально ненаучной формы, прежде всего, поэтических. Порой они дают человеку более полное и глубокое представление о мире, чем научные теории.
Рассмотрим в качестве примера возможные способы описания чёрно-белого рисунка, созданного с помощью средств растровой графики. Его полное и абсолютно точное описание представляет собой прямоугольную таблицу, клетки которой заполнены нулями и единицами. Однако если изображение является хоть сколько-нибудь сложным, представить его по этому описанию практически невозможно. Даже расплывчатая фраза: «Здесь изображён человек», - даёт лучшее представление о рисунке, чем полная, но малопригодная для человеческой психики информация.
Мы можем сделать вывод, что, не отвергая точных описаний, следует искать для них подходящую форму. А, кроме того, крайне желательно, иметь дополнительное средство, позволяющее создавать некий целостный, эмоционально наполненный образ, передающий характер описываемого изображения. Например, звуковым образом некоторого объекта (звуковой моделью) может послужить мелодия.
Данная работа как раз и посвящена разработке подходов к звуковому моделированию графиков математических функций. В связи с выбором изображаемого объекта работа одновременно имеет математические и психолого-педагогические аспекты, и в её основу положен ряд идей математического характера. В частности, как теоретический прообраз звуковой модели функции, используется математическое понятие сплайна.
Термин сплайн произошёл от английского слова spline (рейка, стержень). Этим словом англоязычные чертёжники называли приспособление (гибкую и упругую линейку), предназначенное для проведения через заданные на плоскости точки гладкой кривой. В дальнейшем это название перешло на результат - гладкую кривую. В современной математической практике сплайны составляются из кусков, соответствующих многочленам третьей степени.
По аналогии со сплайнами нами вводятся понятия звукового, вербального и смешанного звуко-вербального сплайнов. Эти понятия являются базовыми терминами, используемыми нами при решении проблемы звукового моделирования функций.
Основные идеи данного исследования таковы.
1. Графики функций выбраны как наиболее удобные объекты для звукового моделирования, поскольку они являются одномерными многообразиями, движение вдоль которых связывает изменение аргумента со временем. Тем самым, изменение независимой переменной моделируется течением времени.
2. Значения ординаты могут быть переданы высотой звука. При этом функция предстаёт перед пользователем как последовательность нот, заменяющих числовые значения. Эту последовательность мы и называем звуковой моделью функции, звуковым сплайном или звуковым графиком. Таким образом, звуковой сплайн представляет собой мелодию, которая генерируется на основе значений моделируемой функции.
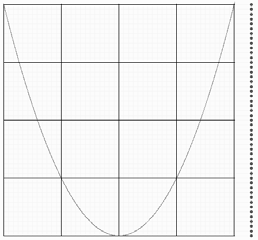
3. Воспроизведение звуковой модели можно сопроводить исследованием функции, а результаты исследования озвучить как комментарий, например, фразами типа: достигнут максимум; функция обращается в нуль; начинается интервал возрастания и т. д. Такой комментарий без звукового графика мы будем называть вербальным сплайном. Соединение звукового графика и вербального сплайна мы называем звуко-вербальным сплайном.
4. Звуковой сплайн можно рассматривать с нескольких точек зрения:
- физически - это последовательность звуков;
- психологически - звуковой образ, обеспечивающий особую форму восприятия функции и графика;
- эстетически - мелодия;
- математически - преобразование непрерывной функции в дискретную последовательность, сопоставляющую моменты времени и ноты;
- алгоритмически - совокупность алгоритмов вычисления или формирования значений функции, исследования функции, преобразования действительных значений в целые и воспроизведения соответствующей мелодии и комментария.
Для выбора наиболее эффективных вариантов создания звуковых моделей функции можно выбирать те или иные виды звуковых рядов.
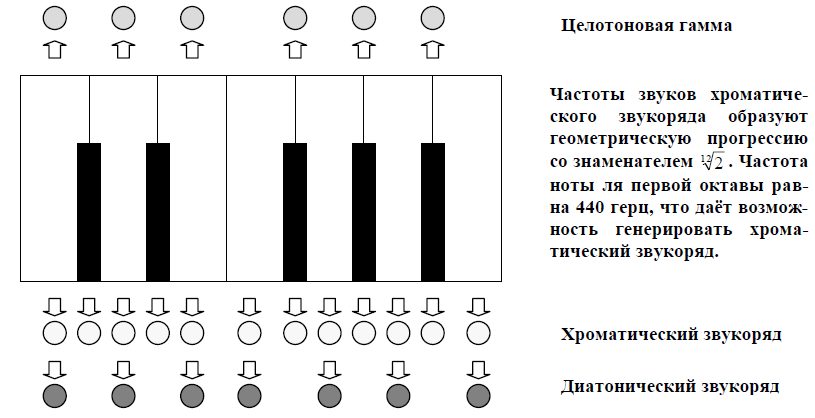
5. Моделируемая функция может задаваться не только аналитически, но и графически. Это открывает возможность создания графического редактора, позволяющего формировать графики функций различной формы.
6. Поскольку нашей основной целью является предоставление пользователям, имеющим ограничения по зрению, возможности чувственного восприятия графиков, крайне желательно обеспечить доступ каждого из этих пользователей к самостоятельному изменению их формы с помощью специализированного графического редактора. Для успешной работы пользователь должен представлять суть действий, которые он может применить к графику функции. При этом он должен мысленно предугадывать результаты своей работы, чтобы позже сравнить ожидаемую форму графика со звуковой моделью и убедиться в правильности своих действий.
Нами выбрана следующая образная схема преобразования графиков, достаточно удобная для пользователей:
- исходные графики, загружаемые в графический редактор и подвергаемые преобразованиям, представляют собой набор из несколько элементарных функций, в число которых входит и константа;
- введены два указателя, обеспечивающих перемещение по графику и управление изменением формы этого графика;
- перемещение горизонтального указателя позволяет выбрать область значений аргумента, вокруг которой будет производиться изменение графика;
- перемещение вертикального указателя поднимает или опускает точки графика в виде бугра или ямы;
- ширина изменяемой области задаётся с помощью специального параметра, названного нами вязкостью.
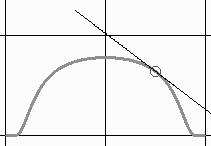

Характер преобразований можно представить себе, осуществляя мысленное поднятие области графика в виде бугра или его опускание в виде ямы. Математические характеристики используемых функций при этом воспринимаются пользователем только на уровне чувственного образа.
Одним из авторов данной статьи (А. К. Новиковым) были написаны две программы, реализующие вышеизложенные идеи.
Первая из этих программ позволяет получить по выбору либо звуковой, либо звуковербальный сплайн для многочленов не выше третьей степени с произвольными коэффициентами.
Вторая программа позволяет:
- озвучивать некоторые часто встречающиеся элементарные функции, такие, например как линейную функцию, её модуль, квадратичную функцию и т. д.;
- строить на экране графики и использовать графический редактор для преобразования в интерактивном режиме исходной функции в функцию произвольного вида;
- сохранять созданную модель и озвучивать её в дальнейшем.
При разработке этих программ и их тестировании проведена серия экспериментов, выясняющих степень эффективности звукового представления функции. Более развёрнутое психолого-педагогические исследование предполагает проведение дополнительной серии экспериментов с участием специалистов по психологии восприятия и тифлопедагогике.
Авторы надеются, что их работа вызовет определённый интерес. Они будут благодарны за любой отзыв об их работе».
Недостатком изложенного в статье метода является то обстоятельство, что в звуковых рядах маловато звуков для гибкого моделирования функций. По этой причине автор статьи продолжил искать новые подходы, предоставляющие доступ к компьютерной графике лицам с дефектами зрения.
5. «ОЩУПЫВАНИЕ» КОМПЬЮТЕРНОГО ИЗОБРАЖЕНИЯ
Вторая работа, направленная на создание программных средств, открывающих доступ к компьютерной графике пользователям с дефектами зрения, была защищена в 2016 году. Речь идёт о дипломной работе Александра Авдеева «Звуко-сенсорное изучение графиков функций».
Эта дипломная работа посвящена разработке подходов к решению проблемы представления графических объектов звуковыми образами, на примере графиков функций, но, как и работа Новикова, она имеет психолого-педагогическое содержание, а не только математическое. Подобным образом в принципе можно озвучивание любые (нематематические) изображения. Работа опирается на одну из психологических теорий первой половины двадцатого века.
Речь идёт, о теории Курта Левина, важном достижении психологической науки, связанном с использованием идей физики. Курт Левин разработал концепцию личности, в основе которой лежит заимствованное из физики понятие поля. Понятие поля с точки зрения Левина представляет собой совокупность взаимосвязанных факторов, состоящую из возможных для данного индивида событий и сил, предопределяющих, какая из возможностей реализуется в поведении индивида. Поведение индивида является внешним выражением событий, происходящих в его психологическом поле. События эти представляют собой либо перемещение из одной области поля в другую, либо изменение самой структуры поля, описываемой Левиным с помощью понятий топологии.
В работе Авдеева метод изучения формы графика, основывается на идеях Курта Левина. Основная мысль такова. Графический объект как бы индуцирует скалярное силовое поле. Величина этого поля убывает с возрастанием расстояния от объекта (изображения) до курсора или пальца пользователя в случае сенсорного экрана. Пропорционально величине поля генерируется звуковой сигнал, который по принципу «тепло - холодно» помогает пользователю, двигаясь по экрану, «ощупать» графический объект. Графики функций выбраны как наиболее простые по форме объекты, а именно линейные многообразия.
После того как в науке было сформировано представление о силовых полях, оказалось, что многие явления могут быть естественным образом описаны именно как поля. В нашем случае речь идёт о поле, связанном с восприятием объекта достаточно сложной формы.
Математическое понятие силового поля (речь идёт не о поле в смысле высшей алгебры) сформировано в рамках математического анализа в векторной форме. При этом под скалярным полем понимают числовую величину, некоторое значение которой сопоставлено каждой точке плоскости или пространства [И. А. Гольдфайн, 1962]. Именно такое математическое поле и служит основой для создания сенсорно-звукового поля, позволяющего «ощупать» графический объект.
При реализации соответствующей программы возникает ряд конкретных проблем вычислительного характера. Первая из них состоит в выборе алгоритма формирования скалярного поля графика, предоставляемого пользователю. Фактически речь идёт об определении расстояния до кривой от каждой точки экранного пространства. При более сложном изображении усложняется и данная проблема.
Одним из вариантов её решения является предварительное сканирование узлов достаточно мелкой решётки. Для каждого узла осуществляется прохождение вдоль графика, приводящее в итоге к определению минимального расстояния от соответствующей точки до кривой. Таким образом, в этом случае заранее формируется массив, задающий скалярное поле с достаточной точностью.
Второй вариант использует прохождение точки по кривой (возможно, с достаточно большим шагом) и определение расстояния в каждый момент перемещения курсора. Здесь важную роль играет время вычисления, поскольку оно может задерживать движение по экрану или отставать от него.
Модификация второго варианта, направленная на ускорение вычислений, состоит в замене кривой на ломаную. При этом определение минимального расстояния до звеньев производится с помощью известной формулы аналитической геометрии.
Кроме проблемы вычисления значений поля расстояний возникает также проблема распределения звуковой интенсивности, то есть проблема преобразования математического поля в поле сенсорно-звуковое.
Наконец ряд проблем связан с навигацией (устранение выхода за пределы экрана) и со скоростью перемещения (она не должна быть слишком быстрой).
В ходе написания дипломной работы была создана работающая версия программы, реализующей идею «ощупывания». Однако желательно было бы продолжить соответствующие исследования и создать более совершенные программные реализации предлагаемого метода.
6. ГРАФИЧЕСКИЙ КОНСТРУКТОР, КАК СРЕДСТВО АКТИВНОЙ РАБОТЫ С КОМПЬЮТЕРНОЙ ГРАФИКОЙ ДЛЯ ПОЛЬЗОВАТЕЛЕЙ С ДЕФЕКТАМИ ЗРЕНИЯ
Наконец, мы подошли к третьей работе, направленной на создание программных средств, открывающих доступ к компьютерной графике пользователям с дефектами зрения. Речь идёт о дипломной работе Николая Шарапова «Графический конструктор для лиц с дефектами зрения», защищённой в 2017 году.
Целью данной дипломной работы является разработка нового подхода, который позволяет лицам с дефектами зрения активно работать с компьютерной графикой и самостоятельно создавать компьютерные изображения. Данная проблема весьма актуальна, поскольку в настоящее время до некоторой степени решены только проблемы работы таких пользователей с текстовой информацией. В то же время невозможность активно работать с компьютерной графикой, что значительно обедняет и затрудняет взаимодействие незрячих с компьютером.
В основу работы положены следующие принципы, которые реализованы в виде отлаженной программы.
1. Посредником между компьютером и незрячим пользователем должна стать инструментальная программа, которая, по сути, является графическим редактором особого вида.
2. Интерфейс данной программы использует только нажатия различных клавиш на клавиатуре и исключает использование мыши. Это сделано по той причине, что незрячему пользователю несравненно удобней работать с клавиатурой.
3. Главной особенностью данной программы является то, что при построении изображения используется только заранее оговорённые геометрические фигуры, например, окружности. По этой причине созданный Шараповым графический редактор можно назвать графическим конструктором, поскольку итоговое изображение как бы конструируется из вполне определённых деталей.
4. Кроме того, в работе с программой заранее оговаривается характер создаваемого изображения. Например, в конкретной реализации программы производится построение рожицы, являющейся традиционной формой детского рисунка.
5. Заранее оговаривается максимально возможное число конструктивных элементов. В данной программе их семь - овал лица, правый глаз, левый глаз, нос, рот, правое ухо, левое ухо.
6. Все элементы изображения занумерованы, что позволяет выбирать и включать в работу нужный пользователю элемент. Например, при нажатии на клавишу с числом «1» пользователь начинает работу с овалом лица.
7. Каждый элемент может подвергнуться однозначно оговоренным изменениям, а именно, увеличение и уменьшение радиуса; перемещение центра окружности в одном из четырёх направлений: вправо, влево, вверх и вниз. Кроме того возможна отмена изменений, произведённых за время последнего контакта с элементом, а также возвращение элемента в исходное состояние.
8. Все действия незрячего пользователя озвучиваются. В частности он оповещается о названии рабочего элемента и о характере последнего действия проведённого им самим. По желанию пользователя может быть произведено озвучивание параметров каждого элемента.
9. Кроме того, программа проводит анализ общей конфигурации построенного изображения и сообщает об этом пользователю. Например, «Изображение находится в пределах нормы» или «Рот вышел за пределы, которые очерчены овалом лица».
10. Предполагается возможность рельефной распечатки изображения с целью осязательного ознакомления пользователя с изображением.
Автору статьи представляется, что и в этом случае желательно было бы продолжить соответствующие исследования и разработки.
7. ЗАКЛЮЧЕНИЕ
В статье излагается несколько идей автора, связанных с тифлопедагогикой и возникших в ходе работы со студентами, имеющими дефекты зрения. Некоторые из этих идей частично реализованы в виде инструментальных программ, созданных в ходе написания дипломных работ, которыми руководил автор данной статьи.
Речь идёт о следующих идеях.
- Использование экрана Алексеева для создания осязательных объектов математического характера, в первую очередь речь идёт о кривых и поверхностях (идея не реализована).
- Разработка электронных документов с блочной структурой и озвучиванием формул и чертежей (дипломная работа Антона Лазарева).
- Передача формы графиков математических функций с помощью звуков различной высоты (дипломная работа Алексея Новикова).
- Сенсорное «ощупывание» изображений с помощью звукового поля различной интенсивности, сформированного по типу «тепло - холодно» (дипломная работа Александра Авдеева).
Предоставление незрячему пользователю графического редактора, организованного по типу конструктора (дипломная работа Николая Шарапова).
Литература
- И. М. Нуркаева. Методические проблемы обучения программированию незрячих и слабовидящих студентов. МГППУ. Труды факультета информационных технологий. Вып. 4, 2009.
- М. Е. Степанов. Метод сложных движений в компьютерной геометрии. Моделирование и анализ данных. Научный журнал. Вып. 1, 2011.
- М. Е. Степанов. Метод криволинейных координат в компьютерной геометрии. Моделирование и анализ данных. Научный журнал. Вып. 3, 2013.
- И. А. Гольдфайн. Векторный анализ и теория поля. М., Физматгиз, 1962.
Информация об авторах
Метрики
Просмотров
Всего: 647
В прошлом месяце: 12
В текущем месяце: 0
Скачиваний
Всего: 261
В прошлом месяце: 4
В текущем месяце: 0