Моделирование и анализ данных
2014. Том 4. № 1. С. 139–161
ISSN: 2219-3758 / 2311-9454 (online)
Некоторые вопросы, связанные с интерполяционным многочленом Эрмита
Аннотация
Общая информация
Рубрика издания: Методика преподавания
Тип материала: научная статья
Для цитаты: Степанов М.Е. Некоторые вопросы, связанные с интерполяционным многочленом Эрмита // Моделирование и анализ данных. 2014. Том 4. № 1. С. 139–161.
Полный текст
1. ВВЕДЕНИЕ
В статье «О прогрессе математики» [Историко-математические исследования. −, 1976] французский математик Ж. Дьедоне писал, «что основной фактор развития математики имеет внутреннее происхождение — размышление о глубокой природе поставленных проблем, независимо от их происхождения. Отметим также часто встречающееся парадоксальное явление, когда внешне пустяковые задачи приводят к красивейшим и мощным теориям. Например, уже с момента возникновения исчисления бесконечно малых располагали вполне удовлетворительными для нужд практики методами приближения корня алгебраического уравнения или же значения определенного интеграла; это, естественно, с самого начала могло бы отвратить математиков от проблемы решения алгебраических уравнений в радикалах или от исследования функции, выражающей длину дуги эллипса, так как, по-видимому, решение этих задач ничего не давало практику, довольствующемуся численными методами. Однако известно, что произошло как раз обратное: упорству математиков, вдохновленных завещанным греками идеалом поиска Истины, свободного от каких-либо практических интересов, мы обязаны рождению теории групп и современной алгебраической геометрии».
Отвлекаясь от бурбакианского утверждения о свободе математики от практических нужд, согласимся с тем, что роль некоторых чисто теоретических задач в истории математики чрезвычайно высока. В этой связи можно отметить, что существуют понятия, занимающие в математике исключительное место и постоянно порождающие важные задачи, влияющие на прогресс математики.
Несомненно, одним из таких понятий является понятие многочлена. Фактически возникнув ещё в древности, в Новое время многочлены приобрели современный вид. Попутно они позволили европейской математике достичь своего первого великого самостоятельного результата - разработки методов решения уравнений третьей и четвёртой степени.
Одно из особо значимых последствий этого открытия состоит в том, что многочлены породили комплексные числа, а, значит, и комплексный анализ. Кроме того, как отмечает Дьедоне, стремление к получению формул для решения в радикалах уравнений степени выше четвёртой привели к возникновению теории групп, которая усилиями К. Жордана, С. Ли, Ф. Клейна и А. Пуанкаре стала идейным стержнем современной математики.
Есть и другой важнейший фактор влияния многочленов на развитие математики. Поскольку многочлены - это функции, для вычисления значений которых достаточно обычных арифметических действий, математики, конечно же, стремились и прочие функции представить в виде близком к многочленам. В результате возникли бесконечные ряды.
В том же духе, духе нахождения если не родства, то близости непрерывных и гладких функций с многочленами, развивались теории интерполяции (отыскания промежуточных значений функции по известным её значениям, то есть своеобразная её реставрация) и аппроксимации (замена одной функции на другую, близкую к исходной). С одной стороны в этой сфере получены выдающиеся теоретические результаты, подобные теоремам К. Вейер- штрасса. А с другой - эти теории являются важнейшей частью вычислительной математики.
В рамках вычислительной математики принято рассматривать интерполяционный многочлен Лагранжа и обобщающий его интерполяционный многочлен Эрмита [Березин, 1962]. Особо следует отметить тот факт, что важным частным случаем интерполяционных многочленов Эрмита являются полиномиальные сплайны.
Цель данной статьи состоит в рассмотрении ряда как теоретических, так и методических аспектов, связанных с использованием интерполяционных многочленов Эрмита.
2. МЕСТО МНОГОЧЛЕНОВ В МЕТОДИКЕ ПРЕПОДАВАНИЯ МАТЕМАТИКИ
Отметим, что понятие многочлена занимает важное место не только в теоретической математике, но и в методике преподавания математических дисциплин. Не претендуя на полноту перечисления разделов математики, при изучении которых центральную роль играют многочлены, выделим только наиболее важные для наших дальнейших целей.
Общеизвестно, многочлены являются обширным полигоном при изучении математического анализа. В частности значительная часть учебных задач, относящихся к дифференциальному исчислению, в том числе к исследованию функций и поиску экстремумов, связана именно с многочленами.

Рис. 1
Мы, однако, сконцентрируем внимание на очень про-стом, но, возможно, ускользающем не только от внимания сту-дентов, но и преподавателей факте. Дело в том, что при введении понятия производной, пусть и неявно, возникает вопрос, который касается интерполяционных многочленов Лагранжа и Эрмита.
Рассмотрим процесс перехода секущей в касательную, раскрывающий геометрический смысл производной. При по-строении касательной к графику функции y = f(x) в точке М0 (х0; у0) сначала проводят секущую через лежащие на графике точки М1 (х1; у1) и М0,. Приближение точки М к точке М0 пре-вращает секущую в касательную.
По сути, уравнение секущей можно записать в виде многочлена Лагранжа первого порядка:
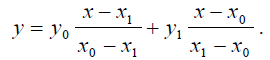
Уравнение же касательной
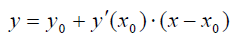 можно рассматривать как многочлен Эрмита в точке хо, для которой заданы значение многочлена и значение его производной.
можно рассматривать как многочлен Эрмита в точке хо, для которой заданы значение многочлена и значение его производной.
В результате процесс превращения секущей в касательную одновременно является процессом перехода многочлена Лагранжа в многочлен Эрмита. Поучительно аналитически зафиксировать динамику этого перехода.
Обозначим разность х1 – х0 через Δх, а разность у1 – у0 через Δу. Тогда уравнение секущей приобретает вид:
![]()
Теперь становится очевидным, что предельный переход при слиянии точек М0 и М1 переводит многочлен Лагранжа в многочлен Эрмита.
Данное наблюдение указывает, что после построения многочленов Лагранжа многочлены Эрмита должны возникать вполне естественным путём при тех или иных формах слияния узлов интерполяции. Учёт этого обстоятельства даёт возможность уяснить наличие глубинной связи между интерполяционными многочленами и рядами Тейлора.
Ещё одной областью математики, неразрывно связанной с многочленами является линейная алгебра. Поскольку совокупность многочленов степени не выше n образует векторное пространство размерности n +1, в этом пространстве можно строить различные базисы. Иногда этот момент затушёвывается тем обстоятельством, что любой другой базис кроме, в высшей степени естественного для многочленов базиса {1, x, x2, … xn}, уходит в тень.
В то же время построение многочленов Лагранжа и Эрмита связано именно с переходам к другим базисам. Так для получения многочлена Лагранжа строится совокупность из n многочленов, каждый из которых обращается в нуль во всех точках хк кроме точки х{, в которой он равен единице. Тем самым строится новый базис. Аналогичная ситуация возникает и при построении многочленов Эрмита.
В этой связи изучение студентами этих двух видов интерполяционных многочленов является хорошим способом практического освоения методов линейной алгебры. Но об этом мы будем подробно говорить ниже. Пока же лишь отметим, что процесс слияния интерполяционных узлов, упомянутый выше, можно рассматривать как переход от одного базиса к другому.
В качестве примера вернёмся к представлению секущей с помощью многочлена Лагранжа, а касательной - с помощью многочлена Эрмита.
Рассмотрим двумерное пространство линейных функций (многочлены степени не выше первой). Каждая из этих функций может быть рассмотрена как многочлен Эрмита с узлом интерполяции хо, то есть может быть разложена по базису {1; (х - хо)}. В этом случае линейная функция принимает вид у = b + к . (х - хо) . Величины b и к являются координатами соответствующей функции в выбранном базисе.
С другой стороны та же функция может быть рассмотрена как многочлен Лагранжа с узлами интерполяции х1 и х2, то есть может быть разложена по базису
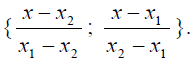 В этом случае линейная функция принимает вид
В этом случае линейная функция принимает вид  Величины у1 и у2 являются координатами соответствующей функции в новом базисе.
Величины у1 и у2 являются координатами соответствующей функции в новом базисе.
Студентам можно предложить в качестве очень простого, но нестандартного задания найти матрицу перехода от первой системы координат ко второй. Для решения этой задачи нужно понимать, что координаты у1 и у2 являются значениями линейной функции в узлах интерполяции х1 и х2, то есть
 Два приведённых преобразования можно записать в матричном виде
Два приведённых преобразования можно записать в матричном виде
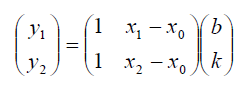
Таким образом, матрица линейного преобразования найдена.
Естественно, переход к многочленам более высоких степеней позволяет ставить значительно более трудные задачи.
3. НЕКОТОРЫЕ НЕСТАНДАРТНЫЕ ЗАДАЧИ, СВЯЗАННЫЕ С ИНТЕРПОЛЯЦИОННЫМИ МНОГОЧЛЕНАМИ
Как часто бывает с математическими конструкциями, инструмент, созданный для решения определённых задач, можно увидеть под несколько другим углом и в результате использовать для иных целей.
В данной статье интерполяционный многочлен иногда служит средством не для интерполяции функций, а для изучения и построения либо последовательностей многочленов, либо функций с особыми свойствами. При этом соответствующая последовательность или же функция может аномально себя вести. Поясним сказанное конкретным примером.
Пример. Пусть на оси абсцисс задано множество точек а1, а2, ... а2n-1, а2n. Если мы рассмотрим функцию y = f1(x), то, построив интерполяционный многочлен Лагранжа, проходящий через точки (ai: fi(ai)), мы решим интерполяционную задачу.
Мы, однако, рассмотрим ещё одну функцию y = f2(x) и будем строить многочлен Лагранжа, в точках с нечётными индексами принимающий соответствующие значения первой функции, а в точках с чётными индексами - второй. Можно ожидать, что подобный многочлен будет «вести себя плохо», поскольку ему «приходится метаться» между двумя функциями. И чем больше количество точек интерполяции, тем хуже поведение многочлена.
Продемонстрируем сказанное с помощью программы, написанной на языке Small Basic. Отметим при этом, что использование подобных программ в учебном процессе может стать важным методическим приёмом, оживляющим абстрактные математические рассуждения и доказательства яркими образами.


В программе рассматриваются две линейные функции ![]() . Абсциссы узлов интерполяции делят отрезок [-1; 1] на равные части. Резкий рост максимумов соответствующих многочленов на этом отрезке виден даже при увеличении числа n от 4 до 6 (рис.2)
. Абсциссы узлов интерполяции делят отрезок [-1; 1] на равные части. Резкий рост максимумов соответствующих многочленов на этом отрезке виден даже при увеличении числа n от 4 до 6 (рис.2)

Рис.2
В целом наша идея состоит в том, чтобы изучать ситуации, в которых последовательность интерполяционных многочленов получает всё больше и больше характеристик, присущих сразу нескольким непрерывным или гладким функциям.
На возможные возражения против целесообразности рассмотрения подобных вопросов можно привести два соображения общего характера. Прежде всего, для современной математики характерен интерес к объектам, когда-то казавшимся аномальными. Достаточно вспомнить отношение Ш. Эрмита к таким «монстрам» как нигде не дифференцируемые функции и сравнить с нынешним интересом к фракталам. Кроме того, нередко возникают ситуации, когда последовательность «хороших» функций к «хорошей» функции не сходится. Однако в итоге удаётся получить совершенно новый и важный объект. В качестве примера можно сослаться на сходимость последовательности функций Дирака к обобщённой функции (см. главу «Теоремы анализа об аппроксимации» из книги [Ленг, 2000]).
В отношении рассмотренного выше примера можно привести более конкретные аргументы о полезности подобных рассмотрений. Пусть мы производим эксперименты (испытания), состоящие в получении значений функции на отрезке [-1; 1].
Пусть далее (см. главу «Интерполирование и приближение функций» книги [Гутер, 1963]) мы последовательно получаем значения функции в узлах Чебышева и строим последовательность интерполяционных многочленов Лагранжа. Тогда для достаточно хорошей функции полученная последовательность многочленов должна равномерно сходиться к этой функции (см. там же теоремы 5, 6 и 7).
В случае, когда последовательность многочленов расходится, желательно по характеру расходимости попытаться выяснить причины такого поведения многочленов. При этом возможными причинами могут быть как «внутренние дефекты» самой функции, так и погрешности при определении её значений. В любом случае изучение характера расходимости имеет определённый смысл.
Ещё один вариант, непосредственно повторяющий ситуацию, описанную в приведённом примере, таков. Пусть наши испытания имеют вероятностный характер, сходный с пове
дением квантово-механических систем. Например, пусть с равной вероятностью мы получаем либо значение функции f1(x), либо значение функции f2(x). Выявление этого обстоятельства также приводит к изучению «плохо ведущих себя» последовательностей многочленов.
4. ТЕРМИНОЛОГИЯ И ВАЖНЫЕ ПРИМЕРЫ
В данном разделе мы введём ряд терминов, которые позволят формулировать наши задачи наиболее кратко. Отметим, что мы отклоняемся от общепринятой терминологии, чтобы лишний раз подчеркнуть тот факт, что, в конечном счёте, нас интересует не интерполяция, а построение новых объектов.
Кроме того, ниже мы рассмотрим некоторые важные для нас примеры и выведем формулы, которые с одной стороны имеют самостоятельное значение, а с другой способы их получения являются пропедевтикой для освоения метода построения интерполяционного многочлена Эрмита в общем случае.
Определение 1. Пусть задана бесконечно дифференцируемая функция действительного переменного y = f(x), а также конечная или счётная последовательность действительных чисел{хi}, где i = 1, 2, 3,... (узлы интерполяции [Гутер, 1963]). Тогда любое значение данной функции или её производной любого порядка в какой-нибудь из точек последовательности называется характеристикой функции y = f(x).
Определение 2. Характеристика функции y = f(x) называется заданной, если её значение должно принимать в соответствующей точке вполне определённое значение.
Определение 3. Если в точке хi заданы характеристики
![]()
то число ki называется глубиной задания характеристик функции в данной точке (кратностью узла интерполяции [Гутер, 1963]). Мы допускаем также и бесконечную глубину задания характеристик.
Задача Эрмита состоит в нахождении функции (а в случае конечного множества узлов - многочлена минимальной степени), имеющей в точках множества {хi} заданные характеристики заданной глубины.
Решением задачи Эрмита в случае многочлена (то есть в случае конечного числа узлов и конечной глубине характеристик в каждом из узлов) как раз и является интерполяционный многочлен Эрмита.
Сразу же отметим, что его построение в любом конкретном случае можно провести «в лоб» методом неопределённых коэффициентов. Пусть множество узлов конечно и сумма глубин характеристик (то есть общее число характеристик) равно п. Тогда многочлен степени п - 1 определяется п коэффициентами, на начальном этапе неизвестными нам. Каждая из характеристик определяет либо значение многочлена, либо значение его производной в одном из узлов.
Соответствующее аналитическое выражение для каждой характеристики представляет собой линейное уравнение с п неизвестными. Всего же таких уравнений в системе также п. Для краткости назовём соответствующую систему линейных уравнений полной характеристикой многочлена Эрмита.
Однако путь к доказательству существования и единственности интерполяционного многочлена Эрмита с помощью построенной системы линейных уравнений не представляется достаточно перспективным. Чтобы показать возможность иного подхода к построению соответствующего многочлена, перейдём к рассмотрению ряда частных, но имеющих большое практическое значение, случаев задачи Эрмита.
Многочлен Лагранжа. Если последовательность чисел {хi} конечна (для определённости состоит из п чисел), а глубина задания характеристик в каждой точке равна единице, мы приходим к задаче о построении интерполяционного многочлена Лагранжа. Система линейных уравнений, являющаяся полной характеристикой многочлена Лагранжа, имеет единственное решение, поскольку определитель матрицы коэффициентов является определителем Вандермонда, который не равен нулю. Тем самым сразу доказывается существование и единственность многочлена Лагранжа.
Как известно, на практике построение многочлена Лагранжа производится без помощи соответствующей системы линейных уравнений. Вместо этого строится совокупность из n многочленов {Li(x)}. При этом многочлен Li(x) обращается в нуль во всех точках хк кроме точки хi , в которой он равен единице. Отметим, что многочлены Li(x) будут встречаться нам и в дальнейшем. По этой причине для них выбрано особое обозначение.
Очевидно, что соответствующий многочлен может быть задан формулой

Фактически совокупность из п многочленов {Li(x)} образует базис в линейном пространстве многочленов степени n - 1. Действительно, любой подобный многочлен имеет в узлах {хi} определённые характеристики и единственным образом представим соответствующей формулой. В нашей терминологии мы можем определить базисные многочлены как многочлены с единственной ненулевой (равной единице) характеристикой.
В дальнейшем во всех задачах мы будем стремиться к построению базисов соответствующего вида - с единственной ненулевой (равной единице) характеристикой для каждого базисного многочлена.
Формула Маклорена. Если последовательность чисел {хi} состоит только из одного числа х1, а глубина задания характеристик в этой точке равна п, мы приходим к задаче о построения многочлена, имеющего в данной точке заданные производные. (Конечные ряды мы будем связывать с именем Маклорена, а бесконечные - с именем Тейлора).
Соответствующий многочлен может быть представлен с помощью формулы Маклорена. С её помощью многочлен р(х) следующим образом выражается через свои характеристики в точке х1:

В данном случае мы снова получаем набор базисных многочленов с единственной ненулевой (равной единице) характеристикой![]()
Поскольку выше мы поднимали вопрос о переходе уравнения секущей (многочлен Лагранжа) в уравнение касательной (формула Маклорена), нельзя не сказать о том, что запись многочлена Лагранжа в форме интерполяционного многочлена Ньютона позволяет осуществить переход от многочлена Лагранжа к ряду Маклорена при стягивании узлов интерполяции в одну точку [Гельфонд, 1967]. К сожалению, объём данной статьи не позволяет затронуть этот важный вопрос подробнее.
Тем не менее, необходимо понимать, что интерполяционные многочлены Эрмита не есть формальное обобщение многочленов Лагранжа, а составляют с ними как бы единый организм, динамика изменений внутри которого определяется предельными переходами. Отметим также, что конкретные задачи, связанные с такими переходами являются хорошими упражнениями при углублённом изучении многочленов.
Ряд Тейлора. Если последовательность чисел {хi} состоит только из одного числа xi, а глубина задания характеристик в этой точке бесконечна, мы приходим к задаче, для решения которой следует построить функцию в виде ряда Тейлора, а затем исследовать сходимость этого ряда.
Формальное построение ряда Тейлора проводится по формуле, обобщающей формулу из предыдущего примера:
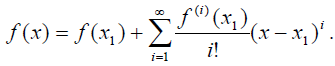
Налицо и счётный набор базисных многочленов с единственной ненулевой (равной единице) характеристикой ![]()
Кубический сплайн. Если имеется только два узла х1 и х2, а глубина задания характеристик в каждом из них равна двум, мы приходим к задаче о построении полиномиального сплайна в виде многочлена третьей степени.
В данном случае не составляет труда построение интерполяционного многочлена Эрмита с помощью системы линейных уравнений, дающей полную характеристику соответствующего многочлена.
Кубическим сплайном называется кривая, являющаяся графиком многочлена третьей степени. Сплайн описывается уравнением у = ax3 + bx2 + cx + d. На него наложены следующие условия. Кривая проходит через точки с координатами (х1, у1) и (х2, у2). В указанных точках функция имеет производные равные р1 и р2 соответственно.
Полная характеристика соответствующего многочлена задаётся с помощью системы линейных уравнений

Легко найти решение системы
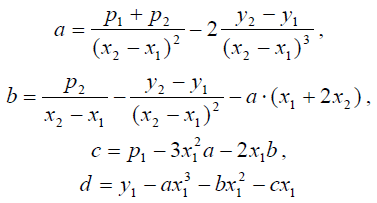
Полученные формулы позволяют вычислить коэффициенты кубического сплайна и построить соответствующую кривую. Однако, как часто происходит при решении задач в лоб с помощью алгебраических преобразований, смысл соответствующих формул часто остаётся скрытым от исследователя.
По этой причине снова будем искать базис, состоящий из четырёх кубических многочленов, имеющих ровно одну ненулевую характеристику. Отметим, что тем самым мы как бы отказываемся от построения конкретного сплайна и привязываем к заданной системе интерполяционных узлов фиксированный базис.
Итак, мы строим многочлены со следующими характеристиками:


Поскольку для многочлена, который вместе со своей производной обращается в ноль в точке х1, число х1 является корнем кратности два, очевидно, что многочлены е3 и е4 представимы в виде:
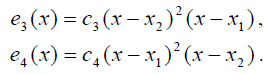
Константы ![]() —— определяются из условия равенства соответствующей производной единице.
—— определяются из условия равенства соответствующей производной единице.
Поскольку многочлен е1 имеет третью степень и корень Х2 кратности 2, он представим в виде
![]()
значение корня 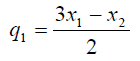 определяется из условия
определяется из условия ![]() , а значение константы
, а значение константы
![]()
С помощью аналогичных соображений устанавливаем, что для многочлена е2
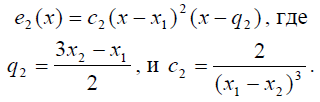
Конечно же, выражения, задающие базисные многочлены, можно получить и с помощью найденных выше коэффициентов a, b, c и d. Для этого необходимо сгруппировать слагаемые, имеющие один из множителей р1, р2, у1 и у2. Но чтобы проделать эти преобразования, нужно заранее осознать важность нахождения соответствующего базиса. Кроме того, формулы будут получены в таком виде, что некоторые свойства базисных многочленов останутся скрытыми.
В силу практической важности кубических сплайнов отметим некоторые характерные особенности построенного нами базиса, связанные с положением на числовой прямой точек ![]() Этот факт мы выделяем по той причине, что корнями многочленов е1(x), е2(x), е3(x), е4(x) являются числа x1, x2, q1 и q2.
Этот факт мы выделяем по той причине, что корнями многочленов е1(x), е2(x), е3(x), е4(x) являются числа x1, x2, q1 и q2.
Для определённости, считая, что x1 < x2, мы можем легко убедиться, что q1 < x1 < x2 < q2. Кроме того,
![]()
Заметим, несколько не в духе современной математики, что подобное расположение указанных точек, на наш взгляд, превращает совокупность базисных многочленов в изящное архитектурное сооружение.
Графики многочленов вообще являются эстетически привлекательными объектами. По этой причине, быть может, следует чаще демонстрировать их студентам, тем более, что современная компьютерная техника позволяет это делать без излишних затрат времени.
Приведём программу для построения соответствующих базисных многочленов, а также результаты её работы.

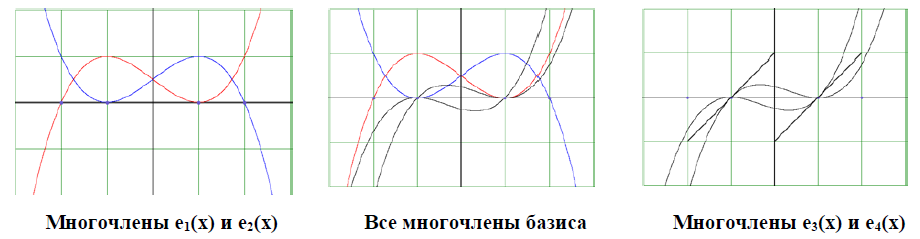
Рис. 3
Переход многочлена Лагранжа в кубический сплайн. Рассмотрим процесс перехода многочлена Лагранжа, имеющего третью степень, в кубический сплайн. Поскольку кубический многочлен Лагранжа имеет четыре интерполяционных узла х1, x2, х3 и х4, то для его перехода в кубический сплайн необходимо осуществить слияние двух пар точек. Для определённости будем считать, что точка х3 переходит в точку х1, а точка хд переходит в точку х2.
Кстати, этот процесс выходит за рамки превращения многочлена Лагранжа в ряд Маклорена, поскольку здесь происходит слияние двух пар точек, но не слияние всех точек в одну.
Рассмотрим, как происходит слияние точек х3 и х1. (Слияние точек х4 и х2 происходит аналогичным образом и приводит к аналогичным результатам). В этом случае необходимо рассмотреть два базисных слагаемых многочлена Лагранжа
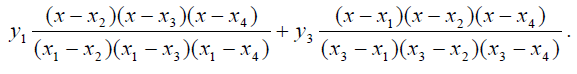
Поскольку происходит слияние точек х3 и х1, обозначим разность х3 - x1 через Δх, а разность у3 - у1 через А у. Тогда наша сумма примет вид
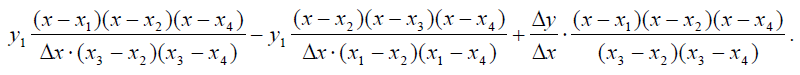
Очевидно, что возникшее третье слагаемое при слиянии точек х3 и х1, а также точек х4 и x2, перейдет в выражение  , которое полностью соответствует базисному многочлену е3(х) для кубического сплайна и его коэффициенту.
, которое полностью соответствует базисному многочлену е3(х) для кубического сплайна и его коэффициенту.
Займёмся преобразованиями двух оставшихся слагаемых. Их сумма записывается в виде

В полученной дроби сокращаются бесконечно малые множители Δх, после чего величина х3 везде заменяется на х1, а величина х4 - на х1. В итоге получаем выражение

В итоге мы видим, что полученное выражение полностью соответствует базисному многочлену е1(х) для кубического сплайна и его коэффициенту.
Итак, многочлен Лагранжа не только благополучно превращается в кубический сплайн, но одновременно и базис многочленов, имеющих ровно одну ненулевую характеристику, переходит в базис, обладающий точно такими же свойствами.
В наших рассуждениях есть некая неточность, похожая на лукавство. Речь идёт о предельном переходе при слиянии точки х3 с точкой х1 и точки х4 с точкой х2. Неясно, к какому значению стремится отношение Δу/Δх. Чтобы устранить эту неясность, необходимо сформулировать теорему, которую мы фактически доказали с помощью своих преобразований.
Теорема. Пусть многочлен Лагранжа с узлами интерполяции х1, х2, х3 и х4 интерполирует дифференцируемую функцию у = f(x). Тогда при стремлении точек х3 к х1 и х4 к х2, многочлен Лагранжа переходит в кубический сплайн, интерполирующий функцию у = f(x) в точках х1 и х2.
Продемонстрируем динамику этого процесса с помощью программы. Положим, что х1 = -1 и х2 = 1. Далее, пусть х3 = х1 + Δх, а х4 = х2 - Δх. Используем в программе функцию вида y = sin πx + 1,5·x2·(x2 - 1)2. Отметим, что выбор этой функции в частности определяется тем, что слагаемое, являющееся многочленом, имеет нулевые производные в точках х1 = -1 и х2 = 1. Таким образом, с помощью подобных слагаемых можно значительно изменить вид графика самой функции, не меняя сплайна.
Работа программа показывает, что при достаточно равномерном распределении узлов интерполяции по отрезку многочлен Лагранжа может достаточно хорошо приближать функцию, поскольку использует информацию о ней в большом числе точек.
При попарном же слиянии точек многочлены Лагранжа сходятся к сплайну, как правило, удаляясь от графика функции.


Рис. 4
Классификация интерполяционных кубических многочленов.
Кубический многочлен Лагранжа имеет четыре интерполяционных узла х1, x2, х3 и x4, которыми он полностью и определяется. Предположим, что узлы упорядочены по возрастанию, то есть ![]() Среди них, естественно, могут быть кратные. Сопоставим каждому типу интерполяционных кубических многочленов последовательности не более, чем из четырёх чисел, равных кратностям узлов, например, последовательности {1, 1, 1, 1} и {1, 2, 1}.
Среди них, естественно, могут быть кратные. Сопоставим каждому типу интерполяционных кубических многочленов последовательности не более, чем из четырёх чисел, равных кратностям узлов, например, последовательности {1, 1, 1, 1} и {1, 2, 1}.
Перечислим все возможные варианты.
1. {1, 1, 1, 1} - интерполяционный многочлен Лагранжа с четырьмя простыми узлами.
2. {2, 1, 1}, {1, 2, 1}, {1, 1, 2} - многочлены Лагранжа с двумя простыми узлами и одним узлом кратности 2.
3. {2, 2} - кубический сплайн.
4. {3, 1}, {1, 3} - многочлены Лагранжа с одним простым узлом и одним узлом кратности 3.
5. {4} - кубический многочлен Маклорена.
Очевидно, что три многочлена из пункта 2 описываются формулами, которые получаются друг из друга перестановкой переменных. Однако при практическом использовании они могут оказаться неравноценными. То же самое можно сказать и о многочленах из пункта 3. Именно эти две группы многочленов, связанные с процессом слияния двух и трёх узлов в один, нами пока не рассмотрены. Без соответствующих формул картина внутренней генетической связи интерполяционных кубических многочленов будет неполна.
Начнём со слияния двух узлов в один, имеющий кратность 2. Кубический многочлен Лагранжа имеет четыре интерполяционных узла х1, x2, х3 и x4. Для определённости будем считать, что точка x4 переходит в точку х1. Узлы х2 и х3 слиянию не подвергаются. В данном случае нам необходимо построить базисные многочлены со следующими характеристиками:
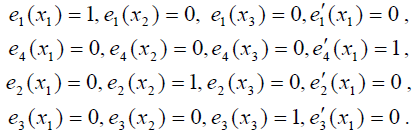
При выводе соответствующих выражений особенно удобна формула дифференцирования произведения: ![]() , поскольку дифференцировать приходится многочлены, представленные в виде произведения двучленов. Очевидно, что многочлен e1(x) имеет вид e1 (x) = c1(x - x2 )(x - x3 )(x - q).
, поскольку дифференцировать приходится многочлены, представленные в виде произведения двучленов. Очевидно, что многочлен e1(x) имеет вид e1 (x) = c1(x - x2 )(x - x3 )(x - q).


Построение двух оставшихся базисных многочленов труда не представляет:

Перейдём к последнему варианту - слиянию трёх точек интерполяции в одну. Для определённости будем считать, что точки х3 и х4 переходят в точку х1, а точка х2 остаётся изолированной. В данном случае нам необходимо построить базисные многочлены со следующими характеристиками:

Очевидно, что 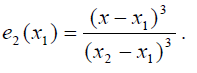

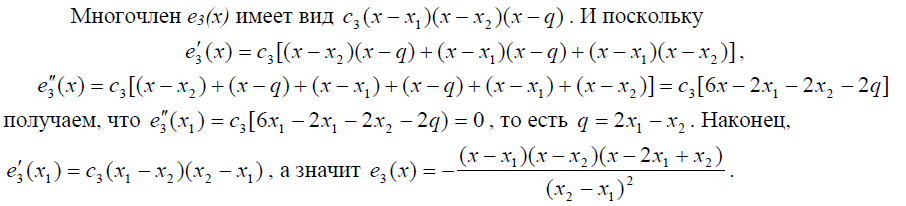

получаем следующие равенства
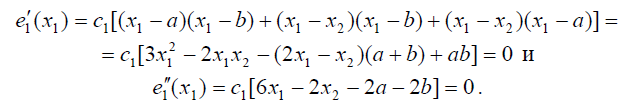
Таким образом, корни a и b удовлетворяют системе уравнений

После простых преобразований получаем, что

По теореме Виета числа a и b являются корнями квадратного трёхчлена
![]()
В итоге получаем, что
![]()
Наконец, поскольку
![]()
получаем окончательную формулу:

С помощью программы на Small Basic продемонстрируем различные виды кубических интерполяционных многочленов. Начнём с прорисовки всех многочленов Маклорена, привязанных к одному из четырёх узлов. Функция останется та же, что и ранее.

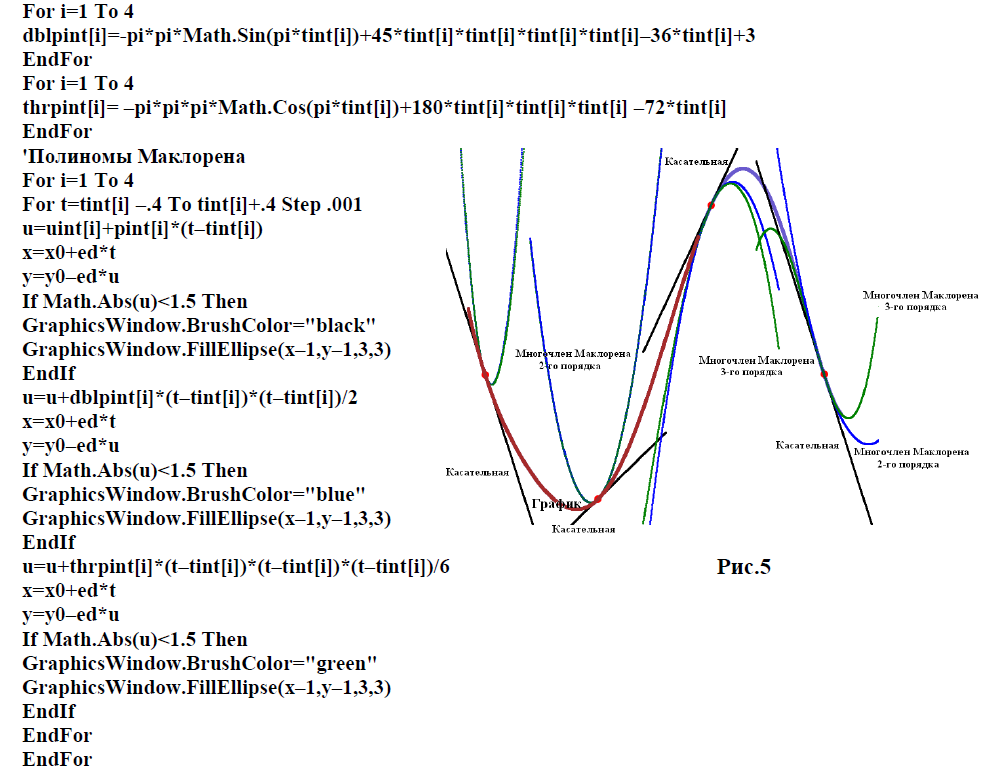
Поскольку многочлены Маклорена приближают функцию особенностью является тесное соприкосновение с функцией.
Далее приступим к прорисовке полиномов Лагранжа вида {2, 1, 1}, {1, 2, 1}, {1, 1, 2}. Соответствующий фрагмент программы является продолжением программы предыдущей. При этом будем считать, что сливаться могут только соседние точки, а крайние точки всегда сохраняют своё положение. Таким образом, мы рассмотрим только следующие схематически изображённые варианты слияния:

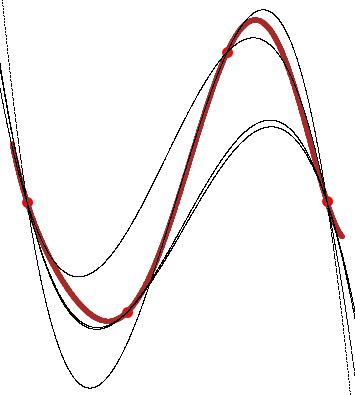
Рис. 6
Многочлены с одним узлом кратности 2 мало отличаются от многочленов Лагранжа и достаточно хорошо приближают функцию.


Наконец построим полиномы Лагранжа вида {3, 1} и {1, 3}. Соответствующий фрагмент программы снова является продолжением предыдущей программы. Будем считать, что крайние точки всегда сохраняют своё положение, а с каждой из них сливаются две промежуточные точки. Таким образом, мы рассмотрим только два схематически изображённых ниже варианта слияния:
![]()

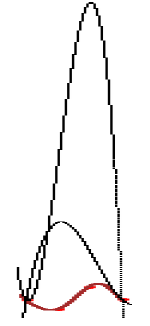
Рис.7
Как и следовало ожидать, полиномы вида {3, 1} и {1, 3} выглядят «плохо», поскольку от полиномов Лагранжа ушли, а к полиномам Маклорена не пришли.
Совокупность базисов полиномов Лагранжа 3-й степени как линейное пространство. Если на числовой прямой задана упорядоченная четвёрка различных точек х1 х2, х3 и х4, то им соответствует базис, состоящий из четырёх базисных многочленов Лагранжа с единственной равной единице характеристикой. Изменение порядка точек в четвёрке приводит к перестановке базисных многочленов, то есть к другому базису.
В случае же различных вариантов слияния указанных точек возникают базисы многочленов Лагранжа с двумя простыми узлами и одним узлом кратности 2, базисы кубических сплайнов, базисы многочленов Лагранжа с одним простым узлом и одним узлом кратности 3, и наконец, базисы кубических многочленов Маклорена. Таким образом, каждому из таких базисов соответствует одна единственная точка четырёхмерного пространства, которое можно назвать пространством узлов интерполяции.
В этом пространстве могут быть выделены линейные подпространства, соответствующие виду слияния соответствующих точек. Например, слияние точек х3 и х4 задаёт трёхмерное подпространство, соответствующее базисам многочленов Лагранжа вида {1, 1, 2}. Уравнение соответствующей гиперплоскости имеет вид хз = хд. Всего же таких гиперплоскостей шесть: х1 = х2, х1 = х3, х1 = х4, х2 = х3, х2 = х4, х3 = х4.
Попарное слияние точек х1 и х2, а также точек х3 и х4 задаёт двумерное подпространство, соответствующее базисам кубических сплайнов. Оно описывается системой из двух уравнений: х1 = х2, х3 = х4. Соответствующее подпространство является пересечением соответствующих гиперплоскостей.
Всего вариантов попарного слияния точек три:
1. Попарно сливаются точки х1 и х2, а также точки х3 и х4.
2. Попарно сливаются точки х1 и х3, а также точки х2 и х4.
3. Попарно сливаются точки х1 и х4, а также точки х2 и х3.
Следовательно, кубическим сплайнам соответствуют три двумерных подпространства. Двумерные подпространства соответствуют и многочленам вида {3, 1} и {1, 3}. Наконец многочленам Маклорена соответствует одномерное пространство или прямая, задаваемая системой уравнений: х1 = х2, х1 = х3, х1 = х4.
Если задана достаточно гладкая функция, с каждым из базисов связан ровно один интерполирующий её многочлен. В соответствии с этим множество интерполирующих многочленов можно сопоставить с четырёхмерным пространством и выделить в нём подпространство кубических сплайнов, подпространство кубических многочленов Маклорена и т. д.
Если же заданы две функции y = f1(х) и y = f2 (х), то каждому базису соответствует два интерполяционных многочлена р1 (х) и р2 (х) . Один из них интерполирует функцию У = f1(х), а второй - функцию y = f2(х) . Таким образом, появляется возможность построения и изучения отображения ![]()
Отметим, не вдаваясь пока в подробности, что всё сказанное может быть обобщено и перенесено на случай n-мерных пространств. При этом на числовой прямой задаётся упорядоченная последовательность различных точек х1 , х2, ... хn. Им соответствует базис, состоящий из n базисных многочленов Лагранжа с единственной равной единице характеристикой.
Далее могут быть рассмотрены все вопросы, связанные со слиянием соответствующих точек в различных вариантах, что в итоге и приводит к построению п-мерного пространства узлов интерполяции и соответствующих подпространств.
Упомянем одну конструкцию, связанную с п-мерным пространством узлов интерполяции. Зададим некоторую достаточно гладкую функцию y = f (х) и поставим в соответствие каждой точке пространства узлов интерполяции значение разделённой разности п-го порядка [Гельфонд, 1967]. Тем самым в пространстве узлов интерполяции будет задано скалярное поле. Оно частично характеризует изначально заданную нами функцию y = f (х), однако не позволяет восстановить её однозначно.
Покажем это на простейшем примере двумерного пространства узлов интерполяции. В этом случае интерполяционным многочленам Лагранжа соответствуют касательные и секущие к графику функции y = f (х). Построение скалярного поля приобретает следующий вид: каждой точке пространства (х1 ; х2) сопоставляется тангенс угла наклона касательной или секущей. В этом случае скалярное поле изображается с помощью поверхности, описываемой функцией от двух переменных х1 и х2.


Рис. 8

Очень кратко упомянём о том, что в n-мерном пространстве узлов интерполяции может быть задано и скалярное поле разделённой разности меньшего порядка, чем размерность пространства узлов интерполяции. Если же в этом пространстве определено несколько подобныХ полей, то могут быть получены и скалярные поля, являющиеся линейными комбинациями исходных полей. В итоге эти линейные комбинации будут соответствовать разностным и дифференциальным уравнениям, точно также как представленная нами выше поверхность соответствует операции дифференцирования.
Сплайн произвольной степени. Если последовательность чисел![]() конечна, а глубина задания характеристик в каждой точке равна двум, мы приходим к задаче о построении полиномиального сплайна степени 2n - 1.
конечна, а глубина задания характеристик в каждой точке равна двум, мы приходим к задаче о построении полиномиального сплайна степени 2n - 1.
Естественно, что и при решении этой задачи следует строить базис, состоящий из 2n многочленов степени 2n - 1, каждый из которых имеет ровно одну ненулевую характеристику. Нитью Ариадны здесь может послужить решение задачи для кубического сплайна.
Рассмотрим узел интерполяции хi . С ним связаны два базисных многочлена с единственной ненулевой характеристикой в точке хi . Пусть многочлен ![]() вместе со своей первой производной обращается в ноль во всех узлах интерполяции кроме точки хi а, кроме того, обладает следующими характеристиками в самой точке
вместе со своей первой производной обращается в ноль во всех узлах интерполяции кроме точки хi а, кроме того, обладает следующими характеристиками в самой точке ![]() Второй многочлен
Второй многочлен![]() также вместе со своей первой производной обращается в ноль во всех узлах интерполяции кроме точки хi, и обладает следующими точке хi характеристиками:
также вместе со своей первой производной обращается в ноль во всех узлах интерполяции кроме точки хi, и обладает следующими точке хi характеристиками: ![]()
Для построения нашего сплайна введём многочлен
![]()
По опыту построения кубических интерполяционных многочленов мы можем теперь предположить, какой вид имеют многочлены ![]()

Таким образом, нам нужно вычислить всего три константы ![]() Займёмся их вычислением.
Займёмся их вычислением.
Поскольку ![]() , должно выполняться условие
, должно выполняться условие


других узлов интерполяции можно получить циклической перестановкой индексов.

5. О МЕТОДЕ ПОСТРОЕНИЯ ИНТЕРПОЛЯЦИОННОГО МНОГОЧЛЕНА ЭРМИТА В ОБЩЕМ СЛУЧАЕ
Метод построения интерполяционного многочлена Эрмита в общем случае достаточно сложен [Березин, 1962]. Наша задача, по крайней мере, в данной статье состоит в том, чтобы подвести студента к пониманию соответствующей проблематики и научить строить интерполяционного многочлена Эрмита самостоятельно, при условии достаточно малого числа узлов интерполяции и достаточно малой глубине задания характеристик искомого полинома.
Для успешного построения интерполяционного многочлена Эрмита студенту необходимо понимать,
1. что строится совокупность базисных многочленов;
2. что каждый базисный многочлен привязан к узлу, в котором имеет одну ненулевую характеристику.
3. как можно записать базисный многочлен, чтобы его характеристики в остальных узлах были равны нулю;
4. какие неизвестные константы входят в состав каждого из многочленов;
5. как определить значения этих констант.
Все эти вопросы решались ранее, и их решение должно послужить примером тех методов, которые нужно применить при построении интерполяционного многочлена Эрмита. Для примера построим интерполяционный многочлен Эрмита для двух узлов с глубиной задания характеристик, равной трём.
Для решения задачи следует построить шесть базисных многочленов. С узлом х1 связаны многочлены е10(х), е20(х) и е30(х). Первый индекс каждого из многочленов указывает на номер узла, в котором он имеет ненулевую характеристику, а второй - на номер этой характеристики, то есть на порядок неравной нулю производной. Таким образом, в узле х2 их характеристики равны нулю, а в узле х1 их характеристики таковы:
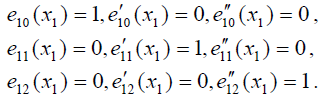
Искомые многочлены имеют вид:
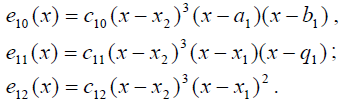
Начнём с последнего многочлена и найдём его первую и вторую производные:
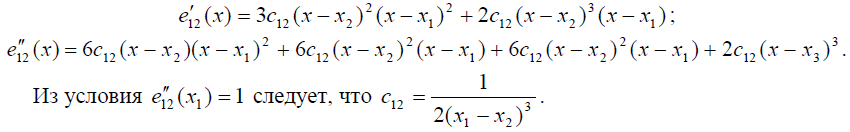
Далее


Наконец, перейдём к полиному е10(х).



6. ВЫВОДЫ
1. Рассмотрены вопросы, связанные с интерполяционным многочленом Эрмита. Полученные формулы могут использоваться в прикладных исследованиях, включая решение задач компьютерной геометрии.
2. Указаны возможные варианты использования интерполяционного многочлена Эрмита в задачах, непосредственно не связанных с интерполяцией конкретных функций.
3. Показано, что материал, группирующийся вокруг вопросов, связанных с интерполяционным многочленом Эрмита, даёт возможность предложить студентам-математикам ряд заданий, требующих одновременного использования знаний из математического анализа и линейной алгебры.
4. Рассмотрена связь соответствующих математических вопросов с программированием. Показано, что использование простых программ в процессе преподавания математики позволяет конкретизировать абстрактные математические понятия в форме визуальных графических объектов.
5. Показано, что использование компьютерных программ позволяет студенту освоиться в предметной области, которой в данном конкретном случае является пространство интерполяционных многочленов.
Литература
- Историко-математические исследования. − М.: Наука, Вып. 21. 1976.
- Березин И. С., Жидков Н. П. Методы вычислений. − М.: Физматгиз, Т. 1, 1962.
- Ленг С. Математические беседы для студентов. − Ижевск: Удмурдский гос. университет, 2000.
- Гутер Р. С., Кудрявцев Л. Д., Левитан Б. М. Элементы теории функций. Справочная математическая библиотека. − М.: Физматгиз, 1963.
- Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. − М.: Физматлит, Т. 1, 1962.
- Гельфонд А. О. Исчисление конечных разностей. − М.: Наука, 1967.
Информация об авторах
Метрики
Просмотров
Всего: 992
В прошлом месяце: 14
В текущем месяце: 1
Скачиваний
Всего: 916
В прошлом месяце: 7
В текущем месяце: 0