Оптимизация параметров обработки сигналов в психофизиологических исследованиях на примере КГР и ФПГ

При анализе физиологических сигналов возникает проблема настройки параметров обработки данных из-за размытости границы между свойствами сигнала и шума, а также фундаментального недостатка объективных критериев качества обработки данных в психофизиологии. В статье описан подход к оптимизации параметров обработки на примере кожно-гальванической реакции (КГР) и фотоплетизмограммы (ФПГ), основанный на использовании значимых для человека стимулов, подобранных на основе биографических данных, что можно рассматривать как критериальную валидизацию. В качестве метрики для оптимизации использовалась частота совпадения выделенных в результате анализа стимулов с априорно заданными (имена людей, включая собственное имя человека, а также выбранные участником эксперимента визитные карточки). Сигналы КГР и ФПГ зарегистрированы с помощью МРТ-совместимого полиграфа в условиях проведения функциональной магнитно-резонансной томографии (N=46 человек). В первой части работы выполнялась оптимизация частотных фильтров и интервалов (эпох) анализа. Установлено, что для анализа амплитудных свойств сигнала КГР оптимальны следующие параметры обработки: фильтры Баттерворта первого порядка, частотный диапазон 0,025—0,25 Гц, интервал анализа 1—7 сот предъявления стимула. Для анализа сигнала ФПГ по длине линии оптимальны следующие параметры обработки: фильтры Баттерворта второго порядка, частотный диапазон 1,25—12,5 Гц, интервал анализа 3—10 сот предъявления стимула. Далее с помощью той же метрики выполнено тестирование нескольких альтернативных способов обработки сигнала: перепад амплитуд сигнала КГР на интервале анализа по сравнению с классическим способом по максимуму амплитуды относительно базового уровня; несколько видов ранжирования реакций в пределах блока стимулов по сравнению с простым усреднением всех реакций. Полученные в работе параметры и способы обработки сигналов демонстрируют универсальность по отношению к разнообразию исходных данных и могут быть применимы в исследованиях прикладной и фундаментальной направленности. Общий подход, описанный в работе, может быть использован также для оптимизации параметров обработки других физиологических сигналов, включая фМРТ.

Введение

Корректная оценка физиологических сигналов, получаемых в ходе регистрации динамики дыхания человека, его и кожно-гальванической и сердечно-сосудистой активности (например, плетизмограммы), представляет интерес, как для фундаментальных, так и для прикладных исследований, проводимых, в частности, в области медицины, криминалистки и других отраслей знаний. В ранее опубликованной статье [9] были представлены результаты экспериментов в области прикладной — криминалистической — психофизиологии, которые свидетельствовали о появлении в отечественных нейробиологических исследованиях новой — нейрокриминалистической — направленности. Упомянутые эксперименты наглядно показали актуальность дальнейшего совершенствования технологии оценки физиологических данных и предопределили необходимость проведения соответствующих дальнейших исследований.

Целью данной работы является апробация такого способа настройки параметров предобработки для физиологических сигналов, который был бы основан на свойствах исходных данных и уменьшил влияние на этот процесс экспериментатора. Такими параметрами в разных исследованиях могут быть, например, частоты фильтрации сигнала, пороги детектирования, интервалы анализа и т.д., призванные сохранить информативный сигнал, но при этом убрать разного рода шум. Однако в силу размытости границы между свойствами сигнала и шума существует проблема влияния субъективных факторов на выбор этих параметров и, как следствие, на экспериментальные результаты. Чтобы избежать ее, исследователи нередко просто оставляют настройки по умолчанию в какой-либо готовой программе обработки, копируют параметры из аналогичного исследования либо обращаются за экспертным мнением. Однако не всегда такой подход работает, особенно если эксперимент не является типовым или проводится на новом оборудовании и/или в необычных условиях. Возможным решением было бы проведение полной процедуры стандартизации измерений, но на практике в настоящее время полноценная стандартизация в психофизиологии затрудняется ограниченностью размеров выборок в силу ресурсоемкости психофизиологического эксперимента, а также фундаментальным недостатком объективных критериев качества измерения и обработки данных. Особенно остро этот вопрос встает при переходе от простого эксперимента на контролируемой группе здоровых добровольцев к актуальной задаче клинических исследований и индивидуальной диагностики [2].

В данной статье представлены результаты исследования подхода к решению этой проблемы на материале зарегистрированных в экспериментах данных кожно-гальванической реакции (КГР) и фотоплетизмограммы (ФПГ). Актуальность работы обусловлена еще и тем, что данные получены с помощью МРТ-совместимого полиграфа (МРТсП) [7] в условиях проведения функциональной магнитно-резонансной томографии при выполнении исследований медицинской и нейрокриминалистической направленности [9], а это требует дополнительного уточнения параметров обработки.

В технических науках в контексте решения аналогичной задачи выделяется ряд подходов.

1. На основе теоретического анализа заведомо известного или хорошо прогнозируемого сигнала. Например, если заранее известен частотный диапазон источника сигнала, а также параметры шума, можно задать параметры частотных фильтров на основе этих данных [6].
2. На основе эмпирической настройки приемной системы по специально сгенерированному тестовому сигналу, совмещенному с источниками помех. Наличие тестового сигнала решает проблему сомнений в том, насколько верна была теоретическая модель процесса обработки данных — если тестовый сигнал детектируется верно, то не так важно, насколько верна была теория обработки и была ли она вообще, но только в том случае, если сам тестовый сигнал и шум соответствуют реальным сигналам. В технике хорошие результаты нередко показывают системы, оптимальность которых не совсем очевидна с точки зрения теории, но являющиеся более простыми в реализации — именно благодаря проверке на тестовом сигнале. Современные искусственные нейронные сети являются примером такого подхода к автоматической оптимизации параметров обработки, причем без анализа этих параметров вручную по причине их слишком большого числа [8].
3. В случае отсутствия возможности создать реалистичный тестовый сигнал (в силу его сложности или малоизученности) прибегают к детектированию сигнала альтернативным способом, так как физические эффекты жестко взаимосвязаны. Таким образом, один из способов регистрации может использоваться в качестве контроля для совершенствования другого способа.

В психологических науках, включая психофизиологию, все эти подходы также применяются [1], но сталкиваются со специфическими сложностями. Например, можно иметь общее представление о частотных параметрах сигнала, но при этом не знать в точности, какая часть этого сигнала важна в конкретном эксперименте, особенно это касается редко используемых диапазонов сигнала. Так, ведутся споры относительно того, следует ли вообще применять частотную фильтрацию к сигналу КГР [21].

Точно также возникают трудности с созданием реалистичного тестового сигнала, так как просто нет достаточных знаний о том, как работает источник этого сигнала — мозг. Тем не менее, стоитотметить появление в последнее время работ по моделированию сигналов КГР [11; 12; 13; 14; 26].

С развитием технических средств получают все большее распространение альтернативные способы контроля сигналов (в психодиагностике такой контроль соответствует термину конкурентной валидности [1]). Например, для взаимного контроля проводится одновременная регистрация одних и тех же источников сигнала несколькими методами: ЭЭГ, МЭГ, экстраклеточная регистрация нейронов, фМРТ, ПЭТ и т.д. Однако такая регистрация, помимо своей очевидной сложности, может быть в принципе невозможна во многих случаях. При этом даже после преодоления технических трудностей и получения физиологических данных по-прежнему остаются вопросы к валидности соотнесения их с психологической феноменологией, в том числе такой принципиально важной, как субъективная значимость экспериментальных заданий, от которой существенно зависит активность мозга, обеспечивающая поведение участников эксперимента [3; 10].

Перспективным может быть подход, выработанный в криминалистической практике использования полиграфа для выявления следов скрываемой информации. Для настройки параметров обработки в этой области науки предложено использовать стандартные тесты с заведомо значимым для человека стимулом [22], что можно рассматривать как критериальную валидизацию на основе биографических данных. Причем для настройки параметров предлагается использовать не простые амплитудные свойства сигнала (на которые напрямую влияет процесс обработки данных), а взаимные соотношения значимых и незначимых сигналов, обработанных одинаковым образом [9]. Таким способом можно попытаться выделить значимый стимул и подсчитать частоту совпадений выделенных стимулов с изначально заданными. В данной работе мы предлагаем использовать эту метрику и расширить ее на более широкий круг задач психофизиологических исследований.

Отдельно стоит рассмотреть важную технологию настоящего времени — искусственные нейронные сети. Применение нейросетей напрямую для обработки данных в психофизиологии сталкивается с рядом трудностей: помимо очевидного дефицита примеров в обучающих наборах данных, которые добываются в весьма трудозатратных экспериментах, остаются проблемы валидности разметки естественных сигналов мозга, а также теоретической интерпретации полученных в итоге результатов. Однако нейросетевой подход закрепил в рутинной практике ряд полезных методических приемов оптимизации, которые ранее были известны, но не применялись так широко и которые можно использовать для работы с классическими способами обработки данных: использование количественных метрик в качестве критерия оптимизации, формализация итерационных приемов (метод градиентного спуска, полный перебор параметров, если это возможно, и т.д.), а также проверка результата на валидационной выборке (что можно поставить в соответствие с критериальной валидностью в психодиагностике [1]).

В данной работе мы предлагаем объединить нейрокриминалистический и нейросетевой подходы. В силу относительно небольшого числа параметров вместо градиентного спуска мы будем применять перебор значений с некоторым шагом, пригодным для графического отображения. Далее значения выходной метрики будут представлены графически, что позволяет выбрать оптимальные параметры обработки визуально. Это соответствует по своей сути методу градиентного спуска (поиск минимума функции ошибки), но при этом позволяет принять более консервативные параметры, потенциально применимые к более широким выборкам, т.е.избежать типичной проблемы переобучения нейросетей, свойственной небольшим выборкам.

В публикациях по обработке сигналов полиграфа обсуждается, в частности, выбор следующих параметров: частотные диапазоны фильтрации и типы фильтров, временные интервалы анализа, а также способ преобразования сигнала КГР и ФПГ в численные оценки величины реакций [5; 19; 20; 21; 27]. Поэтому в данной работе будут проанализированы именно эти параметры. Предполагается, что их оптимизация позволит повысить значение приведенной выше метрики качества обработки данных по сравнению с параметрами, заданными экспертно на основе визуального анализа сигналов. Также мы предполагаем, что полученные параметры окажутся достаточно универсальны и смогут применяться на новых выборках, в том числе в клинических исследованиях.

В криминалистической практике выявлен и используется на практике феномен индивидуальных паттернов реагирования (симптомокомплекс) [4]. В данной работе эта проблематика не рассматривается — стоит задача поиска универсальных параметров обработки, применимых в качестве базовых для групповой обработки данных в когнитивных исследованиях. Также в процессе обработки данных преднамеренно не исключались из выборки участники с нетипичными реакциями или заметными небольшими артефактами в записанном сигнале с целью оптимизации алгоритма обработки таким образом, чтобы он был устойчив к подобным явлениям. Однако в дальнейшем после выявления базовых закономерностей может быть перспективен переход к индивидуальному уровню с учетом паттернов реагирования [23].

Вопрос о конструктной валидности также выходит за рамки данной работы. Предполагается, вслед за [3], что максимальные реакции соответствуют стимулам, имеющим большую субъективную значимость, чем остальные стимулы.

Важным является вопрос релевантности стимулов, т.е. то, что внешний критерий значимости соответствует действительной субъективной значимости. Теоретически может так оказаться, что по каким-то причинам в выборке будет некоторое количество людей, для которых произнесение собственного имени, обозначенного в паспорте, или визитная карточка, выбранная самим участником эксперимента, будут в текущий момент менее значимыми, чем альтернативное имя или визитная карточка. Это может произойти из-за высокой значимости в данный момент какого-либо из альтернативных имен, противодействием исследованию  со стороны участника эксперимента и т.д. Эту проблему можно решить простым количественным способом — оценить на выборке величину частоты совпадений, полученную максимально эффективным методом. Предыдущие исследования показывают (в том числе на той же выборке и на таком же стимульном материале) [9], что частота совпадений по каналу КГР составляет примерно 90—100%. Это означает, что для оставшихся людей несовпадения могут быть обусловлены двумя причинами: как неточностью измерений, так и действительной нерелевантностью стимулов. Однако поскольку число в 10% и меньше составляет относительно небольшую часть выборки, им можно пренебречь в контексте данной работы. Для остальных же участников эксперимента стимулы являются релевантными, так как они стабильно выделяются многими независимыми способами анализа. Таким образом, можно предположить, что оптимизированные по выбранным стимулам параметры могут быть перенесены и на другие субъективно значимые стимулы.

Методика

Участники исследования

В фМРТ-МРТсП-исследовании приняли участие 46 человек (23 мужчины и 23 женщины, студенты технического вуза, возраст 21—23 года), которые сообщили об отсутствии у них каких-либо заболеваний на момент участия в исследовании. Разрешение на проведение фМРТ-МРТсП-исследований было предоставлено этическим комитетом НИЦ «Курчатовский институт».

Процедура исследования

Для проведения экспериментов с применением фМРТ и МРТсП [7] были выбраны парадигма выявления скрываемой информации и соответствующие ей методические средства криминалистических исследований с применением полиграфа — «Тест со скрываемым именем» (ТСИ) и «Тест на знание виновного» (ТЗВ). Первый тест моделировал сокрытие личностно-значимой информации, сохраняемой в памяти человека на протяжении десятилетий. Второй — сокрытие ситуационно-значимой информации, сформированной в памяти человека менее чем за час до эксперимента.

При проведении ТСИ участник эксперимента скрывал от экспериментатора свое собственное имя, предъявляемое в ряду с пятью другими именами: шесть имен предъявлялись в ходе теста пять раз. Ряд имен начинался одним и тем же именем, которое в дальнейшем исключалось из анализа. Все остальные имена (включая имя участника эксперимента) задавали в случайном порядке, который был участнику эксперимента неизвестен. Имена задавали в вопросе: «Вас по паспорту зовут …?». Скрывая свое имя в ряду других имен, участники эксперимента на все вопросы отвечали: «Нет». С целью повышения вовлеченности и внимательности при выполнении теста участник эксперимента после его завершения должен был сказать, сколько раз в ходе ТСИ прозвучало его имя.

При проведении ТЗВ участник эксперимента выбирал в случайном порядке одну из пяти визитных карточек неизвестных ему людей, записывал на бумажку и запоминал фамилию и место работы человека, указанного на этой визитке. Участнику эксперимента давалась установка скрыть от экспериментатора, регистрировавшего фМРТ- и МРТсП-данные, признаки выбранной визитки (фамилию и место работы). Фамилия человека (Ф) предъявлялась участнику эксперимента в ходе теста четыре раза, а место работы (Р) — два. Признаки визитки предъявлялись в следующем порядке: Ф — Р — Ф — Ф — Р — Ф. Перед ними в каждом из шести предъявлений ТЗВ предъявлялись данные с визитки, отсутствовавшей среди пяти предлагаемых на выбор, и исключаемые из анализа. Все остальные задавались в случайном, неизвестном участнику эксперимента порядке в вопросе: «У Вас на визитной карточке была фамилия …?» или «Человек с визитной карточки работает в ...?».

Скрывая признаки выбранной визитки в ряду других фамилий и мест работы, участники эксперимента на все вопросы отвечали: «Нет». С целью повышения сосредоточенности в ходе теста участник эксперимента после его завершения должен был сказать, сколько раз в ТЗВ прозвучали фамилия и место работы человека с визитки.

ТСИ и ТЗВ длились соответственно 6—7 и 8—9 мин. В ходе тестов экспериментатор задавал вопросы с интервалом минимум 10 с, а на практике — 12—20 с, так как производился обязательный учет текущей динамики физиологических показателей участника эксперимента, регистрируемых с помощью МРТсП, чтобы минимизировать наложение случайных флуктуаций сигнала.

Регистрация комплекса физиологических параметров, включая ФПГ и КГР, осуществлялась с помощью созданного в НИЦ «Курчатовский институт» МРТ-совместимого компьютерного полиграфа [7] в условиях одновременной регистрации фМРТ-данных при помощи томографа 3 Tesla SIEMENS Magnetom Verio MR. Подробнее процедура сбора данных описана в [9].

Обработка данных осуществлялась специально разработанным программным обеспечением в среде Python 3.7.4 [28]. Статистические расчеты проводились с помощью открытого программного обеспечения JASP 0.14.1 [29], а численное моделирование фильтров — при помощи TINA-TI v.7.0.30.267 [31] и Octave v.4.4.0 [30].

Наборы данных для оптимизации и валидации

В качестве оптимизационного (обучающего) набора данных были применены тесты ТСИ на мужской и женской выборках (ТСИ М и ТСИ Ж), а также тест ТЗВ на мужской выборке (ТЗВ М). В качестве валидационного набора данных применялся тест ТЗВ на женской выборке (ТЗВ Ж), причем ключи для этого теста не были известны во время подбора параметров. При создании валидационного набора данных преднамеренно не применялось расщепление выборки случайным образом на две статистически однородные половины, так как задача состояла в том, чтобы проверить устойчивость полученных параметров при переходе на новые выборки, которые могут отличаться по динамике физиологических процессов [9].

Обработка данных и процедура оптимизации параметров

Сигнал КГР и ФПГ с аппаратной частотой дискретизации МРТсП 1000 Гц подвергался понижению частоты дискретизации до 100 Гц. Далее производилась цифровая частотная фильтрация при помощи фильтров Баттерворта. После фильтрации выделялись эпохи анализа с заданным интервалом от момента предъявления стимула.

С целью графического отображения выходной метрики фильтрация проводилась итерационно с варьированием параметров фильтров с заранее заданным шагом. Порядок фильтров верхней частоты (ФВЧ) и нижней частоты (ФНЧ) задавался как ряд (1; 2; 3; 4; 8). Частота фильтров для сигнала КГР варьировалась в диапазоне 0,001—1,0 Гц в логарифмической шкале. Промежуточные значения частот были фиксированными и кратными ряду (1,0; 0,63; 0,4; 0,25; 0,16; 0,1) (рис. 2). Частота фильтров для сигнала ФПГ варьировалась в диапазоне 0,02—20,0 Гц в логарифмической шкале. Промежуточные значения частот были фиксированными и кратными ряду (2,0; 1,25; 0,8; 0,5; 0,32; 0,2).

Интервалы анализа также варьировались. Для сигнала КГР начало интервала анализа в секундах от времени предъявления стимула соответствовало ряду (0,0; 0,5; 1,0; 2,0; 3,0). Конец интервала анализа в секундах от времени предъявления стимула соответствовал ряду (4,0; 5,0; 7,0; 10,0; 12,0). Для сигнала ФПГ начало интервала анализа в секундах от времени предъявления стимула соответствовало ряду (0,0; 2,0; 3,0; 4,0; 5,0). Конец интервала анализа в секундах от времени предъявления стимула соответствовал ряду (6,0; 7,0; 9,0; 10,0; 12,0).

В качестве неоптимизированного контроля были приняты параметры, установленные в работе [9] для удобства визуального анализа полиграмм экспертно: фильтры Баттерворта 1-го порядка в диапазонах: КГР — 0,1—1 Гц; ФПГ — 1—20 Гц; интервалы длительностью 10 с, начиная с момента предъявления стимула экспериментатором.

На каждой эпохе анализа вычислялась величина изменения сигнала: подсчитывалась сумма модулей изменения амплитуды на каждом шаге дискретизации. Эта величина в определенном приближении соответствует графической длине линии сигнала (рассматриваемой в ряде работ [20; 27; 5]), но при этом не приводит к возникновению нелинейности в случае маленьких реакций или при изменении масштаба амплитуды. Полученная оценка для сигнала ФПГ умножалась на весовой коэффициент — 1, так как в большинстве случаев личностно значимые стимулы вызывают уменьшение амплитуды ФПГ [16]. Дополнительно для КГР сравнивался классический способ расчета реакций по разнице между базовым уровнем и пиковым значением амплитуды сигнала.

Затем исключались стимулы, начинающие каждый блок предъявлений. Оставшиеся реакции нормировались (z-оценка) на стандартное отклонение по всем реакциям для каждого участника эксперимента и вычиталось среднее арифметическое.

Далее z-оценки реакций подвергались нескольким способам обработки, эффективность которых требовалось проверить в данном исследовании. В качестве базового способа использовалось простое усреднение реакций по предъявлениям для каждого из пяти типов стимулов, и затем производился выбор значимого стимула по максимальной амплитуде реакции. Выделенный таким образом стимул сравнивался с априорно заданным, а далее подсчитывалась частота совпадений в процентах. Эта частота совпадений использовалась в качестве метрики эффективности алгоритма во всех задачах работы.

По полученным картам распределений частоты совпадений визуально определялись оптимальные параметры обработки данных. Как было сказано выше во введении, такой способ не является полностью автоматическим и сохраняется некоторый элемент экспертного подхода, но эксперт при своем выборе получает информацию о распределении метрики качества обработки и может принять обоснованное решение, а также избежать выбора неоптимальных параметров при ограниченном объеме данных, что характерно для автоматического подхода.

После проведения процедуры оптимизации сравнивались результаты обработки с выбранными параметрами и с заданными экспертно ранее в работе [9]. Статистическая проверка различий выполнялась при помощи парного рангового критерия Вилкоксона по всем бинарным значениям совпадений (1) или несовпадений (0). В выборке объединялись данные по мужчинам и женщинам, что в сумме дает N=46. При этом тесты ТСИ и ТЗВ не объединялись, чтобы избежать проблемы инфляции данных.

Далее с помощью того же подхода проверялся еще ряд альтернативных способов обработки. Эти способы описаны в нижеследующих подразделах.

Проверка алгоритма 1: сравнение способов расчета КГР — по сумме модулей изменения амплитуды на каждом шаге дискретизации и по разнице между базовым значением и максимумом амплитуды

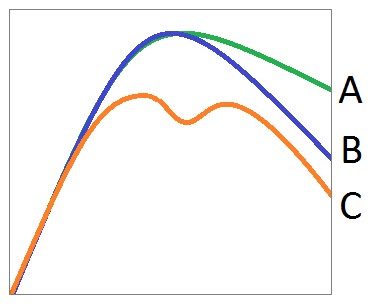
Традиционно в психофизиологических исследованиях фундаментальной направленности при анализе сигналов КГР используют оценку реакций по разнице между базовым значением сигнала (на некотором начальном интервале времени) и пиковым значением амплитуды сигнала [17]. При этом для анализа сигнала ФПГ в ряде работ применяют способ расчета по графической длине линии или близкие к этому варианты [5, 20]. Применение к сигналу КГР того же способа расчета, который применяется к сигналу ФПГ, может быть потенциально полезно в целях унификации, а также возможного улучшения качества обработки данных. Теоретическое обоснование возможного улучшения заключается в учете формы сигнала после прохождения максимума, а также учете двойных пиков (рис. 1). Поэтому в данной работе было решено применить способ расчета по длине линии к сигналу КГР, а затем, имея объективный критерий эффективности алгоритма, сравнить его с классическим.

Рис. 1. Возможное влияние формы сигнала КГР на длину линии на интервале анализа: более резкий спад кривой B при той же величине максимума, что и у кривой А; двойной пик при меньшем максимуме у кривой C

В качестве аналога длины линии вычислялась сумма модулей изменения амплитуды на каждом шаге дискретизации (эта величина с высокой точностью приближается к графической длине линии сигнала для высокоамплитудных сигналов, но при этом избавлена от нелинейности для низкоамплитудных сигналов). Этот метод используется в данной работе для всех вычислений по умолчанию. Интервал анализа использовался тот, который был выбран на шаге оптимизации — 1—7 с (см. раздел «Результаты»).

Для второго (классического) способа использовались несколько интервалов анализа. Для поиска максимального значения применялся тот же интервал 1—7 с, что и для предыдущего способа, а также для сравнения был взят полный интервал 1—10 с. Базовое значение вычислялось как в точке 1 с от предъявления стимула, так и при помощи усреднения на интервалах 0—1 с, 1—2 с и 0—2 с, чтобы проверить влияние способа расчета базового значения.

Проверка алгоритма 2: сравнение способов расчета — простое усреднение реакций и классическое ранжирование реакций внутри блока предъявлений

При вычислении обобщенной оценки для каждого стимула по нескольким предъявлениям может быть реализовано несколько подходов. При автоматическом анализе величины отдельных реакций обычно просто усредняются. Однако при экспертном визуальном анализе полиграмм вначале применяется ранжирование внутри блока стимулов: реакция на «…первый стимул во время теста не оценивается, чтобы уменьшить эффект ориентировочной реакции. Стимул, вызывающий самую сильную реакцию, получает два балла, а стимул, вызвавший следующую, менее выраженную реакцию, получает один балл. Все другие стимулы получают ноль баллов» [18, с. 54]. Такая оценка повторяется для каждого блока стимулов. Далее баллы суммируются между блоками для получения обобщенной оценки для выбранного типа стимулов.

Экспертный подход с ранжированием внутри блока стимулов имеет свое обоснование — резкие случайные выбросы в сигнале, имеющие физиологическую или техническую природу, не смогут получить более двух баллов, тем самым уменьшится их влияние на итоговый результат. Однако процедура ранжирования, в силу перехода на другой тип шкалы, может внести искажения, которые не возникают при простом усреднении. Чтобы решить, какой из этих методов перспективнее применять в практике, мы реализовали автоматическое ранжирование по принципу экспертной оценки, а затем сравнили частоту совпадений, полученную с помощью этого метода и с помощью простого усреднения реакций.

Результаты

Оптимизация сигнала КГР

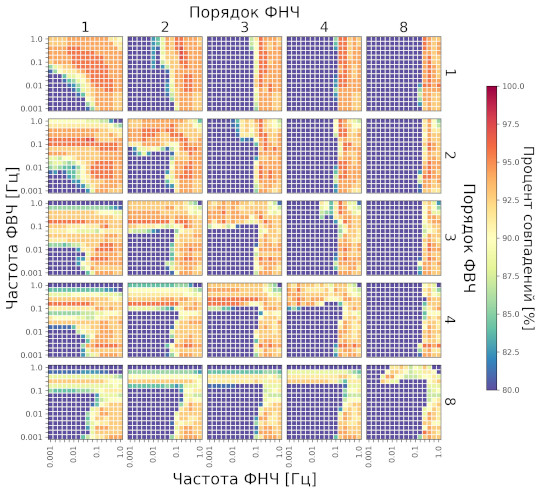
Вначале был произведен выбор порядка частотных фильтров Баттерворта. На рис. 2 приведено распределение выходной метрики (частоты совпадений в процентах) в зависимости от порядка фильтров ФНЧ и ФВЧ, а также от их частоты среза.

Примечание: на всех иллюстрациях наблюдается симметрия распределений (за некоторыми исключениями) относительно диагонали, где частота ФНЧ<ФВЧ и ФНЧ>ФВЧ, что может быть обусловлено особенностями реализации цифровых фильтров, так как фильтрация проводится не однопроходным полосовым фильтром, а двумя фильтрами ФНЧ и ФВЧ отдельно, при этом по амплитуде получившиеся сигналы выравниваются последующей нормировкой.

По рис. 2 видно, что наиболее устойчиво значимые стимулы выделяются при применении фильтров первого порядка — метрика выходит на плато с широким диапазоном возможных частот фильтрации. При этом в случае применения фильтров второго порядка наблюдаются отдельные точки, в которых значение выходной метрики выше. Однако эти выбросы нестабильны и, с высокой вероятностью, не будут воспроизведены в других условиях. Проблема автоматического выбора параметров на небольших выборках обсуждалась выше в разделе «Введение», и в данной работе мы пробуем решить проблему фиксации алгоритма на локальных оптимумах при помощи графической визуализации и выбора более консервативных параметров, имеющих более широкое плато оптимумов. Поэтому для сигнала КГР мы выберем для дальнейшего анализа фильтры первого порядка.

Рис. 2. Распределение частоты совпадений (в процентах) субъективно значимых стимулов, выделенных по сигналу КГР, с априорно заданными по биографическим данным. Каждая точка на карте соответствует определенному диапазону частот фильтрации сигнала КГР, а также порядку фильтра (полный частотный ряд шкалы см. в разделе «Методика»). Приведены объединенные данные для трех тестов тренировочной выборки — ТСИ М, ТЗВ М и ТСИ Ж

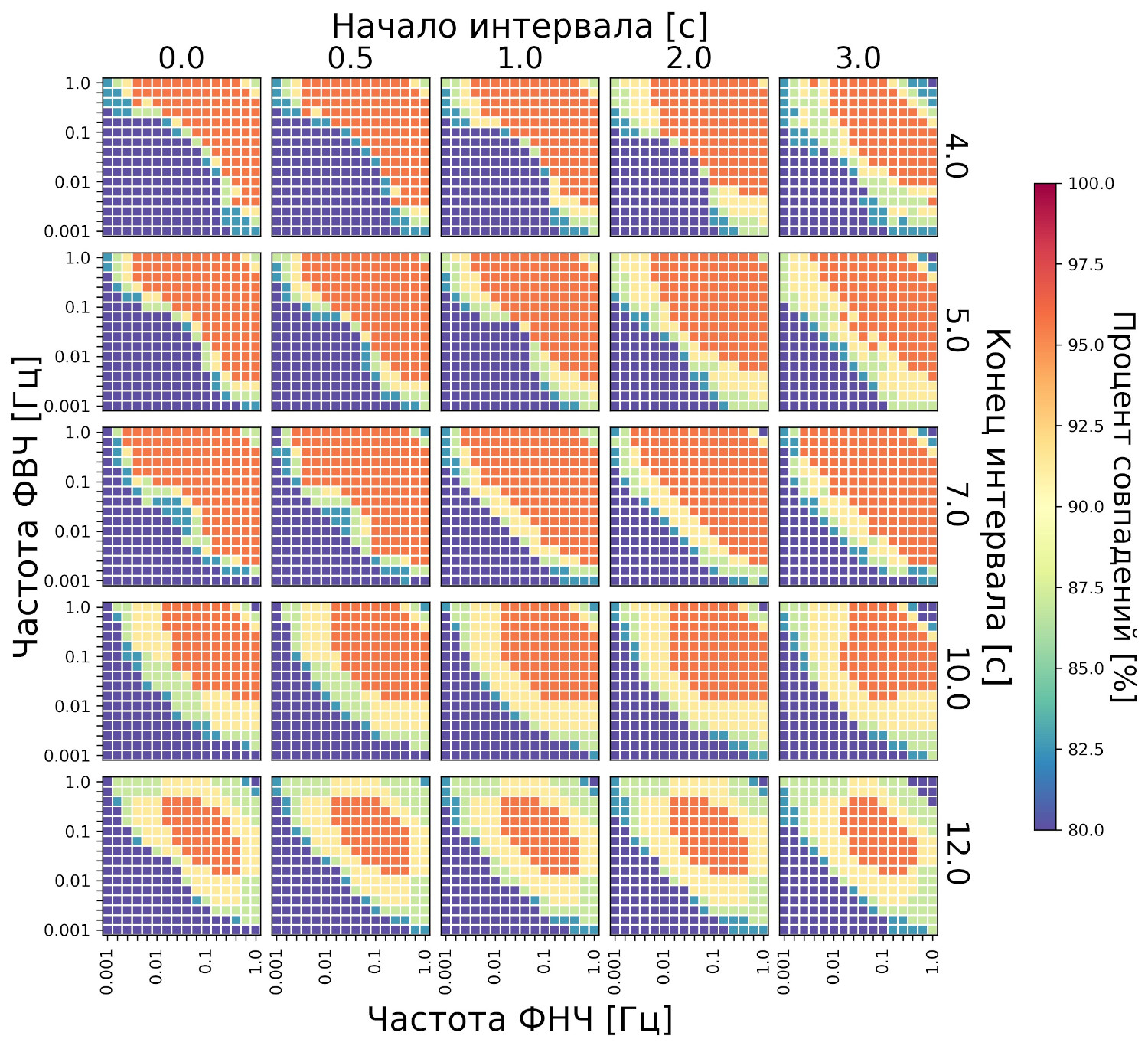
Далее, используя фильтры первого порядка, строим распределение выходной метрики в зависимости от интервалов анализа и также от частот фильтрации (рис. 3). По данному распределению выбираем интервал 1—7 с и частотный диапазон 0,025—0,25 Гц. Интервалы 1—5 и 2—5 с также показывают достаточно плотное распределение выходной метрики, но мы стараемся выбрать максимально широкий интервал для большей универсальности.

Рис. 3. Распределение частоты совпадений (в процентах) по сигналу КГР. Каждая точка соответствует определенному диапазону частот фильтрации сигнала КГР, а также определенному интервалу (эпохе) анализа. Порядок фильтра фиксированный — первый.    Красной и синей рамками выделен интервал 1—7 с и частотный диапазон 0,025—0,25 Гц. Приведены объединенные данные для трех тестов тренировочной выборки — ТСИ М, ТЗВ М и ТСИ Ж

Графическая проверка на ТЗВ Ж (см. рис. 4) показывает, что выбранные значения параметров (интервал 1—7 с и частотный диапазон 0,025-0,25 Гц) находятся вблизи центра плато максимальных значений выходной метрики. Численно значение метрики составило 96% и совпало с таковым для неоптимизированных контрольных параметров (частота 0,1—1 Гц, интервал 0—10 с). При этом для контрольных параметров плато оптимумов имеет меньшую площадь, что может говорить о том, что оптимизированные параметры более устойчивы к помехам, чем неоптимизированные.

Рис. 4. Распределение частоты совпадений (в процентах) по сигналу КГР. Каждая точка соответствует определенному диапазону частот фильтрации сигнала КГР, а также определенному интервалу (эпохе) анализа. Порядок фильтра фиксированный — первый. Приведены данные для валидационной выборки — ТЗВ Ж

Сравнение с контрольными параметрами (табл. 1) показывает, что применение оптимизированных параметров позволило численно улучшить частоту распознавания в одном из тестов (ТЗВ М) до 100%. По остальным тестам результативность не изменилась, но надо заметить, что она и так была высокой.

Статистическая проверка с помощью критерия Вилкоксона по сырым бинарным значениям совпадений и несовпадений (см. раздел «Методика») показала, что различия при применении оптимизированных и неоптимизированных параметров для сигнала КГР статистически незначимы. На валидационной выборке выходные значения совпадают. Это говорит о том, что сигнал КГР имеет высокую устойчивость к изменению параметров обработки.

Таблица 1

Сравнение частоты совпадений для оптимизированных и неоптимизированных параметров обработки КГР с разбивкой на тесты

Оптимизация сигнала ФПГ

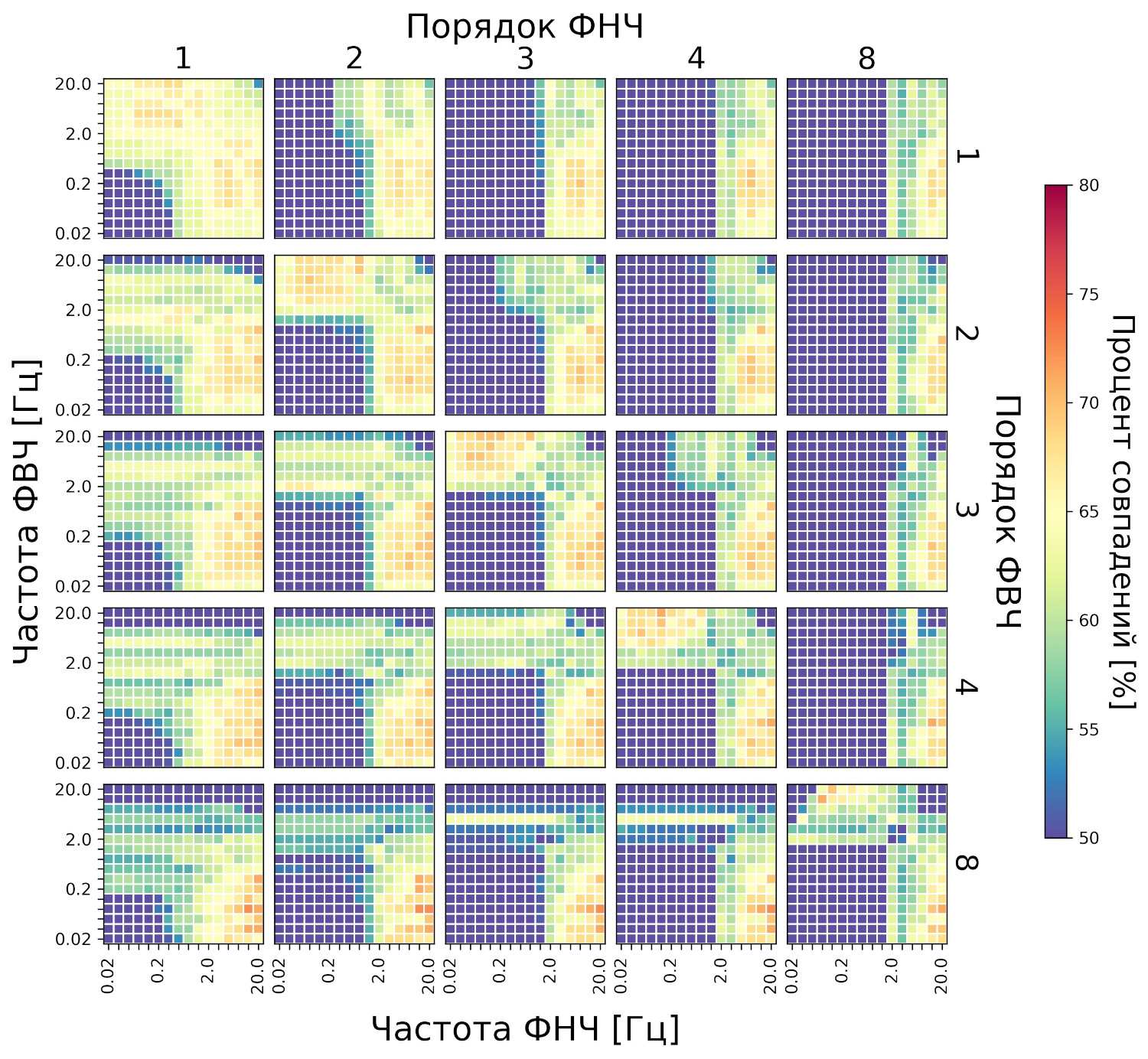
Для сигнала ФПГ вначале также был произведен выбор порядка частотных фильтров Баттерворта. На рис. 5 приведено распределение выходной метрики (частоты совпадений в процентах) в зависимости от порядка фильтров ФНЧ и ФВЧ, а также от их частоты среза.

Рис. 5. Распределение частоты совпадений (в процентах) по сигналу ФПГ. Каждая точка соответствует определенному диапазону частот фильтрации сигнала ФПГ, а также порядку фильтра. Приведены объединенные данные для трех тестов тренировочной выборки — ТСИ М, ТЗВ М и ТСИ Ж

Сигнал ФПГ по сравнению с сигналом КГР показывает меньшую стабильность, и выбрать оптимальные параметры сложнее. Тем не менее, по рис. 5 зафиксируем второй порядок фильтров для дальнейшего анализа — как компромисс между шириной оптимума и пиковым значением оптимума.

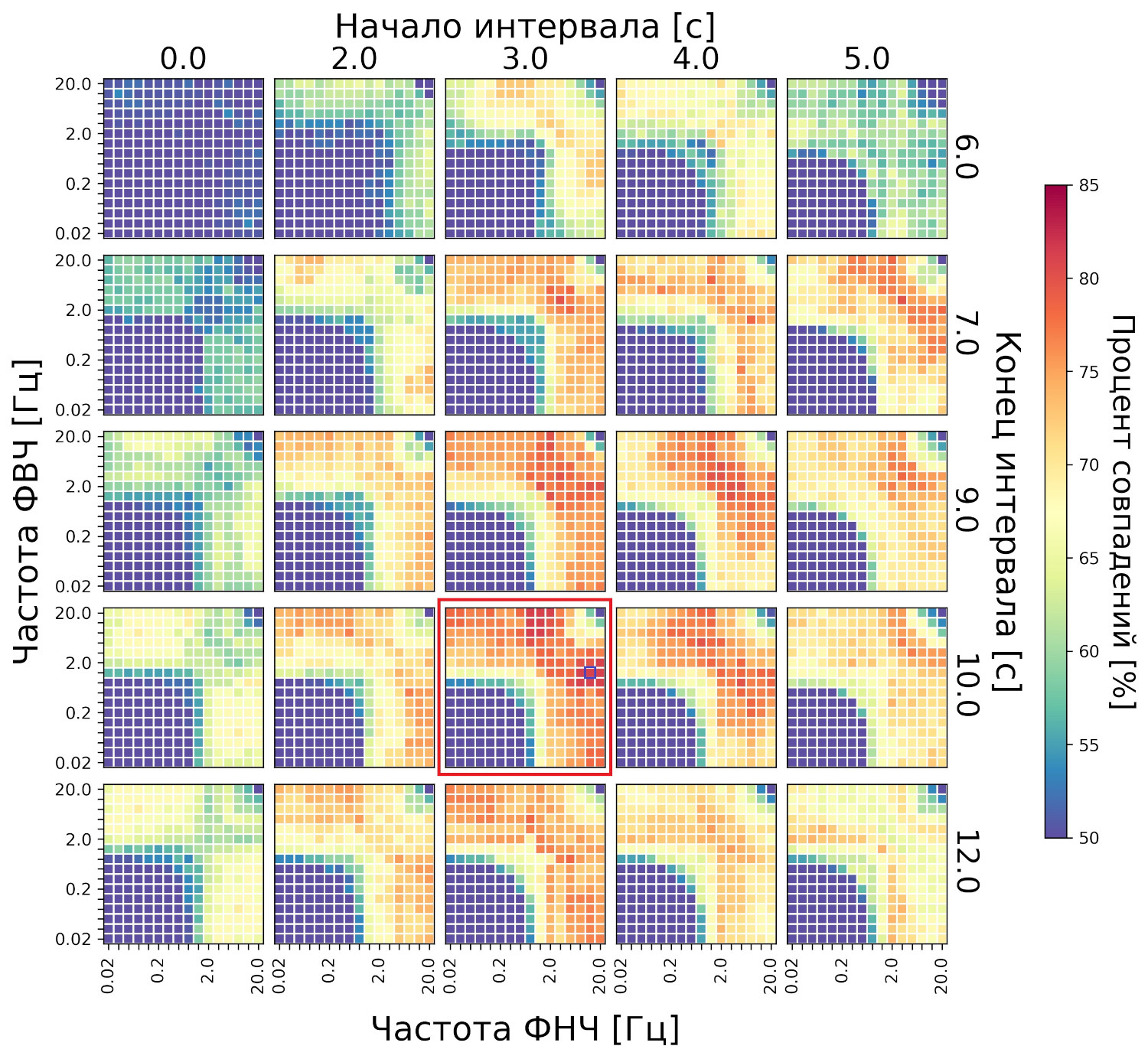
Далее, используя фильтры второго порядка, строим распределение выходной метрики в зависимости от интервалов анализа и также от частот фильтрации (рис. 6). По данному распределению выбираем интервал 3—10 с и частотный диапазон 1,25—12,5 Гц. Интервал 3—9 с также показывает достаточно плотное распределение выходной метрики, но мы стараемся выбрать максимально широкий интервал для большей универсальности.

Рис. 6. Распределение частоты совпадений (в процентах) по сигналу ФПГ. Каждая точка соответствует определенному диапазону частот фильтрации сигнала ФПГ, а также определенному интервалу (эпохе) анализа. Порядок фильтра фиксированный — второй. Красной и синей рамками выделен интервал 3—10 с и частотный диапазон 1,25—12,5 Гц. Приведены объединенные данные для трех тестов тренировочной выборки — ТСИ М, ТЗВ М и ТСИ Ж

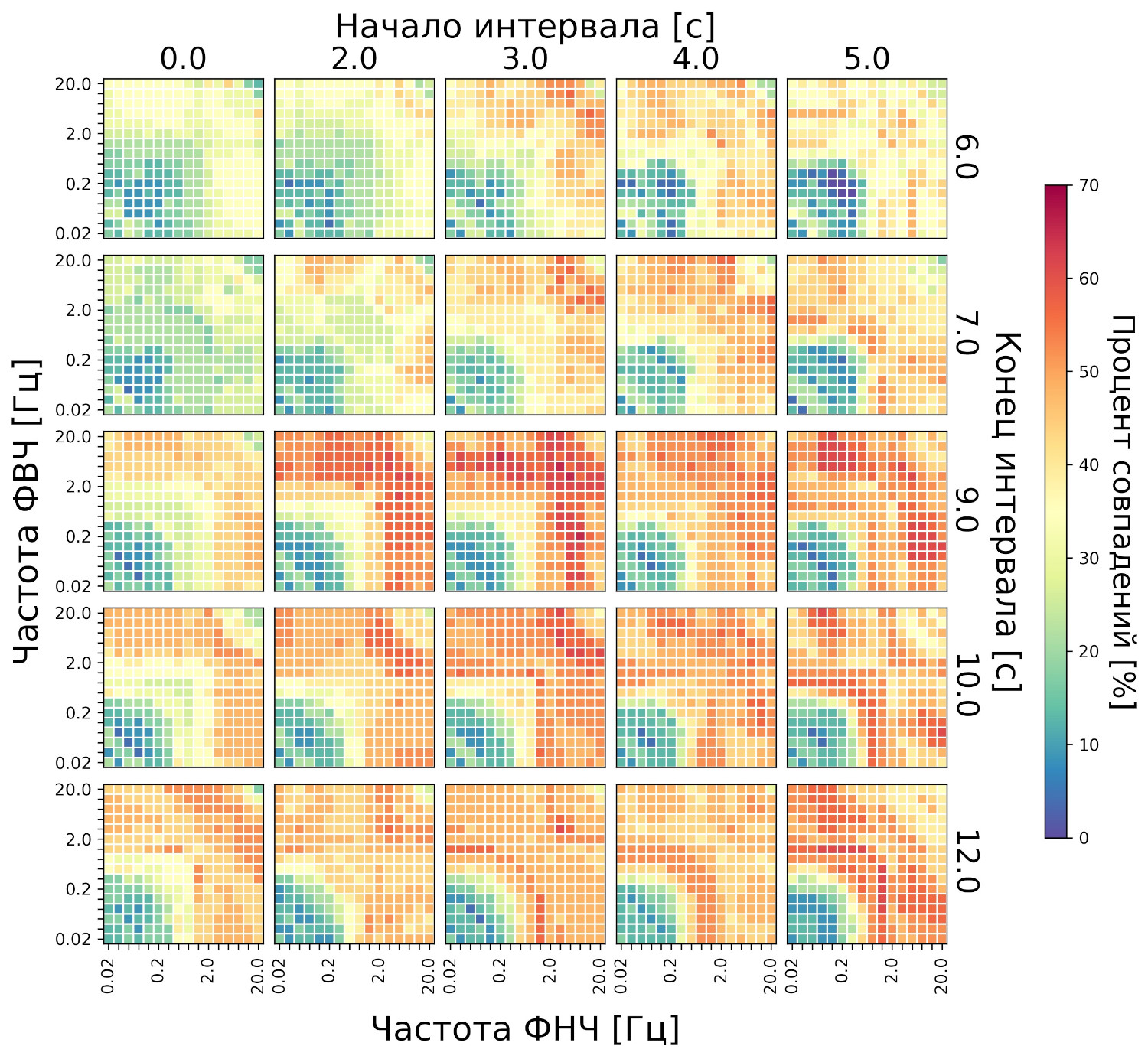
Графическая проверка на ТЗВ Ж (см. рис. 7) показывает, что выбранные значения параметров (частота 1,25—12,5 Гц, интервал 3—10 с) не достигают максимума частоты совпадений. Тем не менее, параметры находятся близко к оптимуму, показывая частоту на уровне 57%, что при пяти альтернативах (т.е. при случайном совпадении 20%) является неплохим показателем. Также полученные значения выше, чем для контрольных параметров (частота 1—20 Гц и интервал 0—10 с). При этом весь тест ТЗВ Ж при любых параметрах показал невысокую частоту совпадений — отдельные разрозненные точки по ТЗВ Ж в максимуме имеют точность лишь 65%.

Рис. 7. Распределение частоты совпадений (в процентах) по сигналу ФПГ. Каждая точка соответствует определенному диапазону частот фильтрации сигнала ФПГ, а также определенному интервалу (эпохе) анализа. Порядок фильтра фиксированный — второй. Приведены данные для валидационной выборки — ТЗВ Ж

Сравнение с контрольными параметрами (табл. 2) показывает, что применение оптимизированных параметров позволило численно улучшить частоту распознавания значимых стимулов во всех тестах (выделено жирным шрифтом).

Статистическая проверка при помощи критерия Вилкоксона показывают большую частоту совпадений с уровнем значимости p<0,05 для оптимизированных параметров. Это верно для тестов ТСИ и ТЗВ, объединенных по мужчинам и женщинам. Отдельная проверка для теста ТЗВ Ж по статистическому критерию не достигает порогового уровня значимости 0,05, но сохраняется численное улучшение (табл. 2).

Таблица 2

Сравнение частоты совпадений для оптимизированных и неоптимизированных параметров обработки ФПГ с разбивкой на тесты

Проверка алгоритма 1: сравнение способов расчета КГР — по сумме модулей изменения амплитуды на каждом шаге дискретизации и по разнице между базовым значением и максимумом амплитуды

В табл. 3 приведены результаты сравнения двух способов расчета численных значений величины реакций КГР — по сумме модулей изменения амплитуды на каждом шаге дискретизации (что в определенном приближении соответствует графической длине линии) и по разнице между базовым значением и максимумом амплитуды. Для первого способа был задан интервал анализа, подобранный ранее как оптимальный. Для второго способа были заданы несколько интервалов для вычисления максимума и для вычисления базового значения.

Результаты показывают, что принципиально эти два способа не отличаются. Наблюдается некоторое численное снижение выходной метрики в одном из тестов при отклонении интервала расчета базового значения и интервала расчета максимума от оптимальных (выделено в таблице жирным шрифтом).

Статистическая проверка выполнялась при помощи критерия Вилкоксона аналогично описанной в предыдущем разделе, отдельно для тестов ТСИ и ТЗВ. Сравнивался первый способ расчета (табл. 3) с остальными. Статистически различия незначимы.

Таблица 3

Частота совпадений для разных способов расчета КГР — по длине линии и по разнице между базовым значением и максимумом амплитуды

Проверка алгоритма 2: сравнение способов расчета — простое усреднение реакций и классическое ранжирование реакций внутри блока предъявлений

Для сигнала КГР (табл. 4) простое усреднение реакций по всем предъявлениям дает устойчиво лучшие результаты по выходной метрике (выделено жирным шрифтом) по сравнению со способами, основанными на ранжировании. Различные виды ранжирования не сильно отличаются между собой.

Статистическая проверка различий между обработкой без ранжирования (усреднением) и вариантами обработки с ранжированием проводилась при помощи критерия Вилкоксона. Данные по тесту ТСИ (объединенная выборка мужчин и женщин) не показывают значимых различий между указанными способами обработки. В тесте ТЗВ обработка КГР без ранжирования показывает лучшие результаты, чем обработка с ранжированием, с уровнем значимости p<0,05, кроме случая «ранжирование 1—0», где p=0,07.

Таблица 4

Частота совпадений для разных способов расчета КГР — с ранжированием внутри блока стимулов и без ранжирования

Для сигнала ФПГ (табл. 5) все способы ранжирования в целом также показывают худший результат по сравнению с простым усреднением реакций за одним исключением — в ТСИ Ж ранжирование 2-1-0 показало численно лучший результат (выделено жирным шрифтом). Этот же способ ранжирования (являющийся классическим) выделяется и на фоне других способов ранжирования. Однако в целом простое усреднение дает лучшие результаты.

Статистическая проверка различий между обработкой без ранжирования (усреднением) и вариантами обработки с ранжированием проводилась при помощи критерия Вилкоксона. В тесте ТСИ (объединенная выборка мужчин и женщин) обработка ФПГ без ранжирования показывает большую частоту совпадений, чем обработка с ранжированием, с уровнем значимости p<0,05, кроме случая «ранжирование 2-1-0». В тесте ТЗВ простое усреднение значимо лучше по сравнению со всеми способами ранжирования.

Таблица 5

Частота совпадений для разных способов расчета ФПГ — с ранжированием внутри блока стимулов и без ранжирования

Обсуждение результатов

Оптимизация сигнала КГР

Полученные нами данные сопоставимы с результатами, описанными в литературе. В работе [24] авторы сравнили Фурье-спектр сигнала КГР в состоянии покоя и во время выполнения стрессогенных когнитивных задач. Они заключили, что спектр электродермальной активности парасимпатической нервной системы может лежать в диапазоне 0,045-0,15 Гц, а симпатической — в диапазоне 0,045-0,25 Гц. Эти диапазоны практически совпадают с результатами, полученными в настоящем исследовании, основанном на симметричном сравнении реакций на стимулы различной субъективной значимости. Некоторая разница по нижней границе (не слишком существенная, что можно видеть по рис. 3) может быть обусловлена тем, что в работе [24] частоты задавались с большим шагом — в виде нескольких предустановленных широких диапазонов. Высокая согласованность результатов тем более примечательна, что она была замечена уже после обработки данных и никак не повлияла на процесс подбора оптимальных параметров фильтрации.

В работе [13] пришли к выводу, что оптимальные параметры фильтра верхних частот следующие: двунаправленный фильтр Баттерворта первого порядка с частотой среза 0,016 Гц (постоянная времени 10 с). Следует заметить, что авторы применяли двухпроходный фильтр, реализованный в пакете Matlab в функции filtfilt[13], при этом два прохода фильтра несколько смещают частоту среза относительно номинально заданной.На рис. 8 показано моделирования амлитудно-частотной характеристики двухпроходного фильтра в программе TINA-TI v.7.0.30.267 [31], такие же результаты получаются при сравнении однопроходной функции filter и двухпроходной filtfilt в Octave v.4.4.0 [30] — происходит смещение стандартной частоты среза по уровню 3 dB почти в два раза. Итоговая частота среза становится равна 0,025 Гц. Это значение численно совпадает с выявленным в настоящей работе. Обзор работы [13] также выполнялся после обработки данных и не влиял на принятие решения об оптимальном значении частоты фильтрации.

Рис. 8. Моделирование амплитудно-частотной характеристики двухпроходного фильтра с частотой среза первого прохода 0,016 Гц (зеленая кривая и красный маркер A). Второй проход тем же фильтром (коричневая кривая и синий маркер B) дает частоту среза 0,025 Гц на уровне 3 dB. По горизонтали задана частота в миллигерцах

Для ФНЧ в работе [13] выбрана частота 5 Гц, не оказывающая существенного влияния на сигнал КГР. Однако при наличии различного рода помех (как, например, при регистрации сигнала в условиях фМРТ-сканирования) имеет смысл ограничивать полосу пропускания только полезным сигналом, т.е. до 0,25 Гц.

Таким образом, можно сделать вывод о сохранении выбранных в процессе оптимизации параметров для применения в дальнейших расчетах. Выбранные параметры в целом согласуются с данными литературы, но при этом имеют следующие преимущества: верхние и нижние границы частотного диапазона максимально близко приближены к диапазону сигнала на основе экспериментальных данных, выбран оптимальный порядок фильтра, оптимизированы интервалы (эпохи) анализа.

Оптимизация сигнала ФПГ

В отношении сигнала ФПГ труднее найти в литературе типичные примеры настройки частотных фильтров, но не в силу недостатка публикаций, а из-за того, что параметры сильно зависят от целей обработки — это может быть как простое вычисление частоты сердечных сокращений, так и сложный анализ формы кривой сигнала ФПГ. Разница верхней границы частот в этих случаях будет варьироваться от единиц до сотен герц. Нижняя граница частот также будет зависеть от целей обработки — требуется ли сохранить форму сигнала или необходимо максимально убрать низкочастотные тренды. Как характерный пример, в работе [25], посвященной изучению формы сигнала ФПГ с клиническими целями, осуществлялась аппаратная фильтрация сигнала ФПГ в диапазоне 0,5—3,4 Гц. Если сравнить эти значения с распределением на рис. 6 и 7, то можно заметить, что они находятся вблизи оптимумов и не слишком сильно отличаются по значению выходной метрики от выбранных при оптимизации параметров, хотя и не достигают максимумов.

В настоящем исследовании стояла прикладная задача подготовки сигнала для вычисления обобщенных показателей, характеризующих субъективную значимость стимула для испытуемого. Поэтому подбор оптимальных значений параметров фильтрации был осуществлен с использованием метрики, основанной на внешнем критерии субъективной значимости стимулов, в то время как в работе [25] в приоритете был визуальный анализ сигнала. Соответственно, оптимизация показала необходимость более сильного подавления низких частот, но при этом пропускания большего диапазона верхних частот, оказавшихся информативными. Выбранные в процессе оптимизации параметры можно зафиксировать для применения в дальнейших расчетах, сохраняя возможность уменьшения интервала анализа до 9 с при необходимости устранения помех.

Проверка алгоритма 1: сравнение способов расчета КГР — по сумме модулей изменения амплитуды на каждом шаге дискретизации и по разнице между базовым значением и максимумом амплитуды

Результаты показали, что указанные два способа анализа дают сопоставимые, статистически не различающиеся величины частоты совпадений (см. табл. 3). Результаты численно совпадают при использовании одинаковых интервалов анализа 1—7 с и выборе в качестве базового значения точки начала интервала — 1 с.

Такие результаты можно объяснить тем, что спад сигнала после прохождения максимума определяется в основном не физиологическими процессами (в случае отсутствия очевидных возмущений), а параметрами фильтра, которые константны. Двойные же пики (см. рис. 1) в анализируемых данных встречались редко и не повлияли на результат.

Некоторое численное снижение (статистически неразличимое) было обнаружено при использовании неоптимизированных интервалов для поиска максимумов и базовых значений (1—10 с и 0—1 с соответственно). Это говорит о том, что использование классического способа анализа по максимумам также может быть чувствительно к интервалам анализа, и методы оптимизации интервалов применимы и к классическому способу.

В качестве заключения можно сказать, что описанные способы анализа показали эквивалентные результаты при использовании оптимизированных интервалов анализа. В дальнейшей работе предполагается применять способ расчета, основанный на «длине линии», для большей унификации процесса обработки данных. Однако классический способ анализа амплитуды КГР остается референсным для сравнения с данными литературы.

Проверка алгоритма 2: сравнение способов расчета — простое усреднение реакций и классическое ранжирование реакций внутри блока предъявлений

Результаты показывают, что как для сигнала КГР (см. табл. 4), так и для сигнала ФПГ (см. табл. 5) простое усреднение дает устойчиво лучшие результаты по выходной метрике. Статистический анализ при помощи критерия Вилкоксона согласуется с этим выводом— различия либо незначимы, либо преимущество у простого усреднения.

Для сигнала ФПГ было замечено, что среди протестированных способов ранжирования классический способ с рангами 2-1-0 показывает лучший результат по сравнению с другими способами ранжирования. Более того, в одном из тестов (ТСИ Ж) такой способ обработки показал результат, численно превышающий простое усреднение. Однако в целом надо сделать вывод, что простое усреднение дает статистически значимо лучшие результаты. Теоретическое объяснение такому результату может заключаться в том, что присваивание высоких рангов в предъявлениях со слабыми реакциями сильнее искажает итоговую оценку, чем случайные выбросы в отдельных предъявлениях в случае простого усреднения.

Выводы

В работе показана оптимизация параметров обработки сигналов КГР и ФПГ при помощи внешнего критерия субъективной значимости стимулов. В качестве метрики использовалась частота совпадения выделенных в результате анализа стимулов с априорно заданными по биографическим данным.

Установлено, что для анализа амплитудных свойств сигнала КГР оптимальны следующие параметры обработки: фильтры Баттерворта первого порядка, частотный диапазон 0,025—0,25 Гц, интервал (эпоха) анализа 1—7 сот предъявления стимула. Возможно уменьшение интервала анализа до 5 с при необходимости устранения помех.

Для анализа сигнала ФПГ по длине линии оптимальны следующие параметры обработки: фильтры Баттерворта второго порядка, частотный диапазон 1,25—12,5 Гц, интервал (эпоха) анализа 3—10 сот предъявления стимула. Возможно уменьшение интервала анализа до 9 с при необходимости устранения помех.

С помощью того же критерия выполнено тестирование нескольких альтернативных способов обработки сигнала.

1. Для оценки амплитуды КГР протестировано использование перепада амплитуд на интервале анализа (сумма модулей изменения амплитуды на каждом шаге дискретизации, «длина линии») по аналогии с обработкой сигнала ФПГ [5]. Сравнение такого способа анализа КГР с классическим — по максимуму амплитуды относительно базового значения — показало их эквивалентность по выходной метрике при использовании оптимизированных интервалов анализа.
2. Протестировано несколько видов ранжирований реакций в пределах блока стимулов по сравнению с простым усреднением всех реакций. Как для сигнала КГР, так и для сигнала ФПГ усреднение дает устойчиво лучшие результаты по выходной метрике, чем ранжирование.

Полученные в работе параметры и способы обработки сигналов КГР и ФПГ, зарегистрированных с помощью МРТсП в условиях проведения фМРТ, находятся в согласии с данными литературы и демонстрируют универсальность по отношению к исходным данным. Это говорит о том, что они могут быть применены для анализа стимулов по субъективной значимости (а возможно, также и по другим характеристикам) в исследованиях прикладной и фундаментальной направленности. При этом в работе не рассматривалась проблематика индивидуальных паттернов реагирования (симптомокомплексов) [4], однако в дальнейшем может быть перспективен переход к индивидуальному уровню с учетом паттернов реагирования [23].

Отдельно следует сказать о работоспособности общего принципа настройки параметров обработки данных, примененного в данной работе. Высокая согласованность результатов с данными других исследований позволяет предположить, что описанный в работе принцип может быть использован для оптимизации параметров обработки других физиологических сигналов, включая фМРТ.

1. Бурлачук Л.Ф. Психодиагностика: учебник для вузов. СПб: Питер, 2006. 351 с.
2. Захарова Н.В., Ковальчук М.В., Костюк Г.П., Бравве Л.В., Кайдан М.А., Карташов С.И., Малахов Д.Г., Холодный Ю.И. Возможности прикладного использования полиграфа для изучения негативной симптоматики больных параноидной шизофренией // Психическое здоровье. 2019. Том 12. С. 50—60. DOI:10.25557/2074-014X.2019.12.50-60
3. Иванов Р.С. Значимость стимула в ситуации психофизиологического исследования с применением полиграфа // Вестник психофизиологии. 2019. № 2. С. 19—30.
4. Иванов Р.С. Индивидуальный симптомокомплекс как инструмент интерпретации результатов психофизиологического исследования с применением полиграфа // Национальный психологический журнал. 2014. Том 3. № 15. С. 90—97. DOI:10.11621/npj.2014.0311.
5. Калафати А.Ю. Исследование длины линии ФПГ и дыхания для различных диапазонов оценки // Детекция лжи. 2021. Том 4. С. 33—40.
6. Колосовский Е.А. Устройства приема и обработки сигналов. М.: Горячая линия-Телеком, 2007.
7. Малахов Д.Г., Холодный Ю.И. Система одновременного контроля и оценки динамики физиологических процессов в условиях проведения магнитно-резонансной томографии человека. Патент № RU2756566C1.
8. Николенко С.И., Кадурин А.А., Архангельская Е.О. Глубокое обучение. СПб.: Питер, 2019. 480 с.
9. Холодный Ю.И., Малахов Д.Г., Орлов В.А., Карташов С.И., Александров Ю.И., Ковальчук М.В. Изучение нейрокогнитивных процессов в парадигме сокрытия информации // Экспериментальная психология. Том 14. № 3. С. 17—39. DOI:10.17759/exppsy.2021140302
10. Alexandrov Y.I. How we fragment the world: the view from inside versus the view from outside // Social Science Information. 2008. Vol. 47. № 3. 419—457. DOI:10.1177/0539018408092580
11. Bach D.R., Flandin G., Friston K.J., Dolan R.J. Modelling event-related skin conductance responses // Int. J. Psychophysiol. 2010. Vol. 75. 349—356. DOI:10.1016/j.ijpsycho.2010.01.005
12. Bach D.R., Flandin G., Friston K.J., Dolan R.J. Time-series analysis for rapid event-related skin conductance responses // J. Neurosci. Methods. 2009. Vol. 184. P. 224—234. DOI:10.1016/j.jneumeth.2009.08.005
13. Bach D.R., Friston K.J., Dolan R.J. An improved algorithm for model-based analysis of evoked skin conductance responses // Biol. Psychol. Vol. 94. P. 490—497. DOI:10.1016/j.biopsycho.2013.09.010
14. Bach D.R. A head-to-head comparison of SCRalyze and Ledalab, two model-based methods for skin conductance analysis // Biol. Psychol. 2014. Vol. 103. P. 63—68. DOI:10.1016/j.biopsycho.2014.08.006
15. Barzegaran E. EEGSourceSim: A framework for realistic simulation of EEG scalp data using MRI-based forward models and biologically plausible signals and noise // J. Neurosci. Methods. 2019. Vol. 108. P. 328—377. DOI:10.1016/j.jneumeth.2019.108377
16. Council N.R. The polygraph and lie detection. Washington: The National Academy Press, 2003. P. 314. DOI:10.17226/10420
17. Dawson M.E., Schell A.M., Filion D.L. The electrodermal system // Handbook of psychophysiology / J.T. Cacioppo, L.G. Tassinary, G.G. Berntson (Eds.). Cambridge University Press, P. 159—181. DOI:10.1017/CBO9780511546396.007
18. Department of Defense, DC. The accuracy and utility of polygraph testing. Washington, D.C.: Natioflal Institute of Justice, United States Department of Justice, 1984. Vol. 13. P. 54.
19. Elaad E., Ben-Shakhar G. Covert respiration measures for the detection of concealed information // Biological Psychology. 2008. Vol. 77. № 3. P. 284—291. DOI:10.1016/j.biopsycho.2007.11.001
20. Elaad E., Ben-Shakhar G. Finger pulse waveform length in the detection of concealed information // International Journal of Psychophysiology. 2006. Vol. 61. 226—234. DOI:10.1016/j.ijpsycho.2005.10.005
21. Kalafati A., Krapohl D.J. The difference between the manual and automatic settings for the electrodermal channel and a potential effect on manual scoring // Polygraph & Forensic Сredibility Assessment: A Journal of Science and Field Practice. 2018. Vol. 47. № 1. P. 37—44.
22. Kovalchuk M.V., Kholodny Y.I. Functional magnetic resonance imaging augmented with polygraph: new capabilities // Biologically Inspired Cognitive Architectures 2019. BICA 2019. Advances in Intelligent Systems and Computing. 2020. Vol. 948. P. 260—265. DOI:10.1007/978-3-030-25719-4_33
23. Orlov V., Kartashov S., Malakhov D., Kovalchuk M., Kholodny Y. Evaluation of fMRI Data at the Individual Level // Biologically Inspired Cognitive Architectures 2021. BICA 2021. Studies in Computational Intelligence. 2022. Vol. 1032. DOI:10.1007/978-3-030-96993-6_42
24. Posada-Quintero H.F., Florian J.P., Orjuela-Cañón A.D., Aljama-Corrales T., Charleston-Villalobos S., Chon K.H. Power Spectral Density Analysis of Electrodermal Activity for Sympathetic Function Assessment // Ann. Biomed. Eng. Vol. 44. P. 3124—3135. DOI:10.1007/s10439-016-1606-6
25. Reguig M., Reguig F. Photoplethysmogram signal processing and analysis in evaluating arterial stiffness // International Journal of Biomedical Engineering and Technology. 2017. Vol. 23. DOI:10.1504/IJBET.2017.10003507
26. Tronstad C., Staal O.M., Saelid S., Martinsen O.G. Model-based filtering for artifact and noise suppression with state estimation for electrodermal activity measurements in real time // Proceedings of the 2015 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), 2015. DOI:10.1109/EMBC.2015.7318961
27. Vandenbosch K., Verschuere B., Crombez G., DeClercq A. The validity of finger pulse line length for the detection of concealed information // International Journal of Psychophysiology, 2009. Vol. 71. № 2. P. 118—123. DOI:10.1016/j.ijpsycho.2008.07.015
28. Anaconda [Электронный ресурс]. URL: www.anaconda.com (дата обращения: 12.11.2022).
29. JASPTeam. JASP (Version14.1), 2020. [Электронный ресурс]. URL: https://jasp-stats.org/ (дата обращения: 12.11.2022).
30. Octave [Электронный ресурс]. URL: www.octave.org (дата обращения: 12.11.2022).
31. TINA-TI [Электронный ресурс]. URL: www.tina.com (дата обращения: 12.11.2022).