Экспериментальная психология
2018. Том 11. № 2. С. 77–94
doi:10.17759/exppsy.2018110206
ISSN: 2072-7593 / 2311-7036 (online)
Диагностика по тестовым траекториям: метод паттернов
Аннотация
Общая информация
Ключевые слова: диагностика когнитивных способностей, диагностика операторов сложных технических систем, адаптивное тестирование, IRT, метод паттернов
Рубрика издания: Математическая психология
Тип материала: научная статья
DOI: https://doi.org/10.17759/exppsy.2018110206
Для цитаты: Куравский Л.С., Юрьев Г.А., Ушаков Д.В., Юрьева Н.Е., Валуева Е.А., Лаптева Е.М. Диагностика по тестовым траекториям: метод паттернов // Экспериментальная психология. 2018. Том 11. № 2. С. 77–94. DOI: 10.17759/exppsy.2018110206
Полный текст
Введение
Компьютерное тестирование широко используется как средство психологических и педагогических измерений, для диагностики различных заболеваний, а также с целью определения уровня компетенций и степени сформированности навыков, необходимых для выполнения той или иной деятельности. Качество и достоверность получаемых результатов определяются технологиями тестирования, которые в последние десятилетия стали предметом активных научных исследований.
До второй половины прошлого века тесты строились на основе классической теории тестирования (Gregory, 2007; Gulliksen, 1950), в основе которой лежит теория погрешности измерений, заимствованная из физики: полагалось, что измеряемые характеристики имеют некоторые «истинные» значения, искажаемые случайными и систематическими погрешностями. Этот подход получил определенное распространение, однако его практическому применению препятствовала недостаточная надежность и универсальность применяемого подхода, проблемы при сравнении сходных особенностей тестируемых, выявленных с помощью разных методик, и невозможность оценки валидности тестов.
Для преодоления указанных проблем в 60-е г. XX в. была разработана новая технология тестирования, основанная на латентно-структурном анализе (Item Response Theory — IRT)1 (Baker, 2001; Wright, Masters, 1982). Базовый тезис этого подхода, сформулированный Г. Рашем (Rasch, 1980), заключается в том, что вероятность правильного ответа на задание определяется разностью количественных оценок трудности теста и уровня знаний, способностей, навыков или других конструктов и выражается функцией сигмоидного типа. В зависимости от условий прикладной задачи, на практике используются и другие технологии, построенные на основе данного тезиса (Thompson, Weiss, 2011; Torre, Patz, 2005). Кроме того, с опорой на принципы IRT и оценки максимального правдоподобия, реализована концепция адаптивного тестирования, согласно которой, с целью обеспечения наилучшей дифференциации, испытуемым на каждом шаге тестовой процедуры подбираются задания с трудностью, соответствующей текущей расчетной оценке его конструктов.
Применению технологии IRT сопутствует ряд существенных ограничений, включая:
— «статичность» оценок: игнорирование того факта, что результат тестирования вследствие усталости испытуемых и других факторов может, вообще говоря, существенно изменяться со временем;
— невозможность полезного использования при построении расчетных оценок информации о времени, затрачиваемом на выполнение заданий, и динамике получаемых результатов;
— необходимость выполнения достаточно большого числа заданий для получения оценок с приемлемой достоверностью.
Одна из основных проблем адаптивного подбора заданий, опирающегося на оценки IRT, обусловлена приблизительным равенством вероятностей правильного и неправильного выполнения заданий, что делает результаты тестирования зависимыми, в основном, от посторонних случайных факторов, не связанных с измеряемыми конструктами.
Указанные проблемы сделали актуальной разработку новых подходов к решению рассматриваемой задачи. В 2010—2012 гг. был разработан метод адаптивного тестирования (Куравский и др., 2013; Куравский и др., 2012; Куравский, Юрьев, 2011а; Куравский, Юрьев, 2011б; Куравский, 2017; Kuravsky et al., 2015; Kuravsky et al., 2015), построенный на применении идентифицируемых марковских моделей с непрерывным временем и байесовской классификации. Этот метод стал основой для разработки новой технологии адаптивного обучения (Куравский и др., 2016)
Его особенностями, обеспечивающими преимущества перед аналогами, являются:
— выявление и использование при построении расчетных оценок временной динамики изменения способности справляться с заданиями;
— возможность учета при построении расчетных оценок времени, затрачиваемого на выполнение заданий;
— возможность исследования временной динамики конструктов как в дискретной, так и в непрерывной временной шкале;
— меньшее по сравнению с другими подходами число заданий, которое следует предъявлять испытуемому для оценки конструктов с заданной точностью, что ускоряет процесс тестирования;
— получение распределения вероятностей возможных результатов теста в качестве конечного результата;
— развитая техника идентификации параметров моделей.
Как развитие этого результата в 2017 г. предложен новый вариант марковской модели адаптивного тестирования с дискретным временем (Куравский и др., 2017), предполагающий оценки конструктов с использованием предельных распределений вероятностей пребывания в состояниях, вычисленных с помощью матриц вероятностей перехода. Преимущества такого подхода по сравнению с адаптивным тестированием на основе IRT заключаются в следующем:
— оценка не выводится из локальных сопоставлений текущих измерений оценок и трудностей с использованием модели Г. Раша, но учитывает всю наблюдаемую историю выполнения тестовых заданий, которая включает в себя распределение успешных и неуспешных выполнений заданий и их порядок, а также время, затраченное на выполнение тестовых заданий;
— оценки основаны на прогнозируемых результатах в будущем, при условии, что время тестирования не ограничено и они не используют локальные (т. е. для определенного задания) сравнения, основанные на модели Г. Раша, которые могут быть неустойчивыми;
— количество заданий, которые необходимо выполнить, существенно меньше;
— выбранные трудности заданий связаны с историей выполнения тестовых заданий и не зависят напрямую от текущих приближенных оценок уровней достижений испытуемых;
— существует возможность учитывать изменение трудности конструктов для испытуемого во время процедуры тестирования из-за усталости и других причин;
— имеется возможность самообучения, которая приводит к улучшению характеристик модели адаптивного тестирования во время ее эксплуатации;
— существует процедура идентификации модели, основанная на простых и доступных результатах наблюдений.
В то же время представленный подход может рассматриваться как расширение IRT, поскольку модель Г. Раша используется в качестве его компонента.
Преимущества предложенного варианта марковской модели по сравнению с предшествующими решениями состоят в следующем:
— вместо марковских процессов с непрерывным временем используются марковские процессы с дискретным временем, однако в новой адаптивной модели время, затрачиваемое на выполнение заданий, учитывается с помощью ограничений на время пребывания в состояниях и переходов в состояния-«ловушки».
— допустимы политомические задания.
Применение разработанных марковских моделей для решения задач диагностики требует настройки их параметров по репрезентативным эмпирическим данным достаточно большого объема, которые не всегда доступны. Поскольку на практике часто возникает необходимость решать задачи диагностики, располагая ограниченными результатами наблюдений, необходима разработка методов, полезных в подобных условиях. Кроме того, для обеспечения надежности построение диагностических выводов, особенно в случае малых выборок, желательно выполнять непосредственно по эмпирическим данным, минимизируя необходимые теоретические построения.
В качестве решения, согласующегося с указанными требованиями, в этой работе представлен метод паттернов для диагностики испытуемых по так называемым тестовым траекториям — последовательностям значений, представляющим результаты выполнения тестовых заданий в порядке их появления. Тестовые траектории могут содержать как временные ряды данных, разбитых по субтестам, так объединенные временные ряды, собранные в общую последовательность. В отличие от традиционных методов рассматриваемый подход позволяет:
— учитывать динамику результативности выполнения тестовых заданий;
— работать с диагностическими характеристиками, непрерывно зависящими от времени (что, как правило, имеет место при диагностике операторов сложных технических систем);
— строить на своей основе адаптивные технологии тестирования, позволяющие, в зависимости от результатов конкретного испытуемого, изменять как количество предъявляемых тестовых заданий, так и их содержание, добиваясь заданного уровня надежности диагностической оценки.
2. Метод паттернов для диагностики по тестовым траекториям
Диагностика заключается в отнесении испытуемых к одному из заранее определенных классов i е {0, ..., z}. Для решения задачи необходима база данных, содержащая выборку паттернов, которые представляют динамику результатов выполнения заданий из различных субтестов и относятся к одному из распознаваемых классов испытуемых. В ряде прикладных задач для центров кластеров паттернов, относящихся к рассматриваемым классам, а также — в случае диагностики операторов сложных технических систем — для каждого паттерна выборки могут храниться атрибуты, относящиеся к распознаваемым классам. Примерами таких атрибутов могут служить выборочные функции распределения расстояний до центров кластеров распознаваемых классов.
После выполнения испытуемым определенного тестового задания, для содержательного набора данных, представляющего результаты его тестирования, накопленные к контрольному моменту времени, с помощью указанной базы данных, в зависимости от прикладной задачи, определяются:
— вычисленные в определенной далее метрике расстояния до центров кластеров паттернов, относящихся к распознаваемым классам, вместе с их атрибутами — выборочными функциями распределениями расстояний до центров этих кластеров, или
— ближайший в той же метрике паттерн, после чего рассматриваемому испытуемому приписываются соответствующие атрибуты.
Сравниваемый с паттернами фрагмент результатов тестирования должен быть сопоставим с ними по числу тестовых заданий и времени их выполнения.
Алгоритмические аспекты решения задачи представлены следующими шагами.
Шаг 1: нормализация. До выполнения указанных вычислений временные ряды, представляющие динамику результативности выполнения тестовых заданий, если это необходимо, приводятся в единую шкалу, где максимум соответствует единице, а минимум — нулю.
Шаг 2: устранение избыточной информации. В случае данных, разбитых по субтестам или представленных несколькими измеряемыми параметрами, избыточная информация, содержащаяся в указанных временных рядах, устраняется с помощью метода главных компонентов (Principal Components Analysis) (Vidal, Yi Ma, Sastry, 2016; Kong, Hu, Duan, 2017). Для этого вычисляются матрицы взаимных корреляций значений временных рядов, решается алгебраическая проблема собственных значений и выяснятся, насколько можно понизить размерность собственного подпространства исследуемых параметров, так, чтобы после этого в нем содержалась достаточно представительная (на практике от 70% и выше) часть изменчивости наблюдаемых параметров. Для каждого из выбранных собственных направлений этого подпространства (главных компонентов) по одной из наибольших компонентных нагрузок выбирается представитель из числа субтестов или регистрируемых параметров (переход в базис главных компонентов нецелесообразен из-за неопределенной содержательной интерпретации главных компонентов и, в ряде прикладных задач, отсутствия точной синхронизации исследуемых процессов для разных испытуемых по времени). Цель этого этапа — оставить только относительно независимые характеристики, заменяя группы существенно зависимых одним представителем, чтобы избежать искажений, обусловленных совместным влиянием сильно зависимых характеристик на последующих этапах.
Шаг 3: переход к интегральным характеристикам для временных интервалов посредством дискретного вейвлет-преобразования. Временные ряды, представляющие исследуемые тестовые процессы, заменяются наборами вейвлет-коэффициентов, полученных в результате кратномасштабного анализа (Multiresolution Analysis) (Grieb, 2010). При этом исходные процессы как функции времени заменяются интегральными характеристиками временных интервалов области их определения. Кроме того, становится возможной существенная экономия (примерно на порядок) в числе коэффициентов, необходимых для корректного представления процесса. Благодаря принятым в кратномасштабном анализе правилам привязки вейвлет-коэффициентов к фрагментам временного ряда, снимаются проблемы, связанные с необходимостью точной синхронизации процессов, относящихся к разным однотипным тестовым процедурам, по времени (поскольку наиболее значимые коэффициенты, относящиеся к относительно продолжительным интервалам времени, практически не чувствительны к небольшим временным сдвигам). Длина используемых на последующих этапах вейвлет-представлений процессов может быть существенно (примерно на порядок) меньше, чем длина соответствующих им исходных временных рядов без потери точности оценок.
Шаг 4: вычисление матриц взаимных расстояний. Для каждого исследуемого субтеста или параметра вычисляется матрица взаимных расстояний между полученными на этапе 3 вейвлет-представлениями исходных процессов для различных испытуемых. Размерности этих матриц равны объему выборки анализируемых испытуемых. Указанные матрицы взаимных расстояний для всех рассматриваемых субтестов или параметров складываются, формируя суммарную матрицу взаимных расстояний между испытуемыми.
Шаг 5: многомерное шкалирование с целью анализа взаимного расположения испытуемых в пространстве приемлемой размерности. Вычисленное расположение испытуемых в результирующем пространстве многомерного шкалирования (Multidimensional Scaling) (Borg, Groenen, 2005; Trevor, Cox, 2001; Young, 2013) далее используется для определения расстояний между испытуемыми с целью принятия диагностических решений. Размерность пространства шкалирования определяется исходя из условия достаточной дифференциации выборок испытуемых, относящихся к различным распознаваемым классам.
Шаг 6: вычисление расстояний до центров кластеров паттернов или ближайшего паттерна для испытуемого по результатам выполнения последовательности тестовых заданий. В случае выборок паттернов достаточно большого объема определяются расстояния до центров кластеров паттернов. Они вычисляются по данным многомерного шкалирования, полученным на шаге 5. В случае малых выборок паттернов определяется ближайший паттерн, что может выполняться двумя способами: или непосредственно через вычисление ближайшего в евклидовой метрике вейвлет-представления паттерна, или через определение ближайшего в евклидовой метрике паттерна в результирующем пространстве многомерного шкалирования.
Шаг 7: вероятностные оценки распознавания классов испытуемых. Вероятностные оценки распознавания определяются с помощью выборочных функций распределений Fi(X) Fi(X) евклидовых расстояний XX до центров кластеров паттернов, принадлежащих к соответствующему распознаваемому классу i ∈ {0, ..., z}, в пространстве многомерного шкалирования. Вычисленные значения Pi = 1 - Fi (ri) Pii = Fi (ri) , где riri— евклидово расстояние оцениваемого испытуемого до центра i-го кластера в пространстве многомерного шкалирования, интерпретируются как вероятностные оценки принадлежности к указанным классам. Их распределение по классам 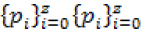 характеризует надежность полученной классификации.
характеризует надежность полученной классификации.
Диаграмма потоков данных (data flow diagram), представляющая рассмотренные выше этапы решения задачи, приведена на рис. 1.
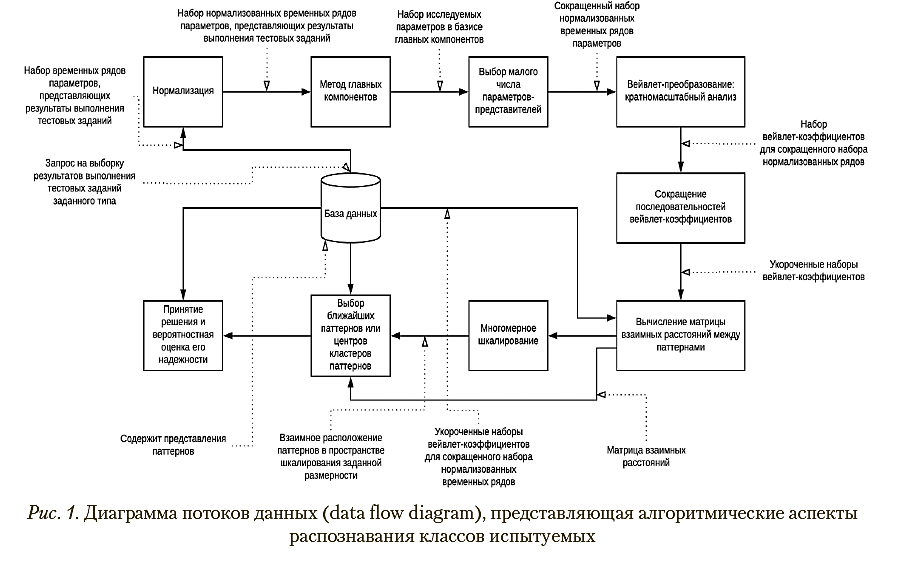
3. Диагностика когнитивных способностей: пример практического применения
Проиллюстрируем особенности представленного подхода на примере диагностики когнитивных способностей по результатам разработанного в Институте психологии РАН теста (Baker, 2001), состоящего из 8 субтестов, которые оценивают различные типы интеллектуальных показателей, и содержащего в общей сложности 128 заданий. Субтесты содержат от 11 до 25 заданий. Выборка испытуемых включала 204 человека. В качестве распознаваемых классов, использованных для настройки параметров диагностической процедуры, рассматривались группы испытуемых с высоким и низким общим уровнем когнитивных способностей, выявленные по итоговым результатам тестирования и включавшие по 45 человек.
В последующем анализе паттерны представлены испытуемыми, а исследуемые параметры — результатами субтестов, которые имеют вид временных рядов, составленных из бинарных значений (1 — испытуемый справился с заданием, 0 — не справился). Для вычислений использовались пакет для статистического анализа STATISTICA и программное обеспечение собственной разработки, реализованное в среде графического программирования LabVIEW.
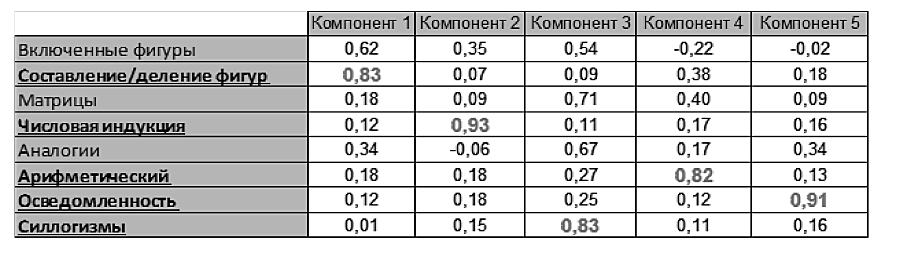
Анализ методом главных компонентов выявил, что представленная суммарной дисперсией изменчивость результатов тестирования на 83% объясняется влиянием 5 латентных компонентов, которые, в свою очередь, учитывая значения компонентных нагрузок, показанных в табл. 1, могут быть представлены 5 субтестами: «Составление/ деление фигур», «Числовая индукция», «Арифметический», «Осведомленность» и «Силлогизмы».
Таблица 1
Компонентные нагрузки, определенные для 8 субтестов
методом главных компонентов
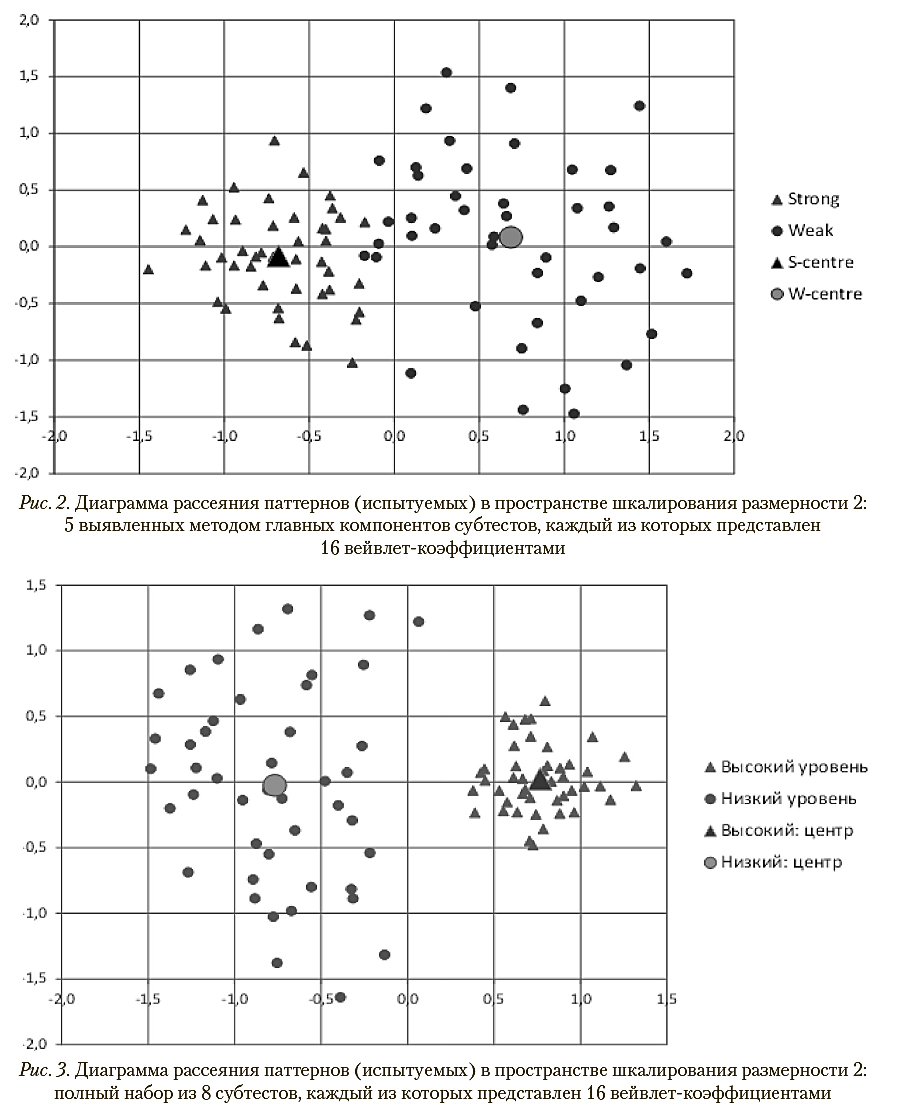
Кратномасштабный анализ, вычисление матриц взаимных расстояний и шкалирование позволили построить диаграммы рассеяния в пространстве размерности 2, приведенные на рис. 2 и 3. Повышение размерности пространства шкалирования для рассматриваемой задачи нецелесообразно, поскольку используемая размерность обеспечивает нахождение паттернов разных классов в непересекающихся областях (рис. 3). Качественное сравнение диаграмм рассеяния позволяет заключить, что уменьшение числа субтестов в данной задаче с 8 до 5 сохраняет возможность разделения рассматриваемых классов испытуемых, однако вероятность ошибки при этом несущественно возрастает (с 0% до 3%).
Уменьшение числа вейвлет-коэффициентов, используемых при построении матриц взаимных расстояний, с 16 до 4 практически не влияет на возможность разделения классов (рис. 4). Таким образом, как и в большинстве подобных задач, небольшое число первых вейвлет-коэффициентов содержит всю существенную информацию для анализа.
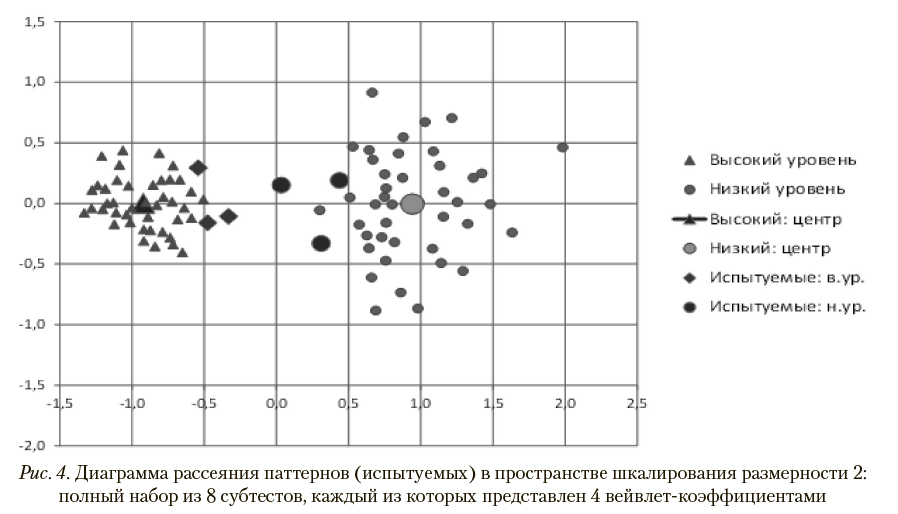
На рис. 5 и 6 представлены выборочные функции распределения расстояний до центров кластеров, составленных испытуемыми рассматриваемых классов, в пространстве шкалирования, показанном на рис. 4. Соответствующие им графики выборочных плотностей вероятности приведены на рис. 7 и 8.
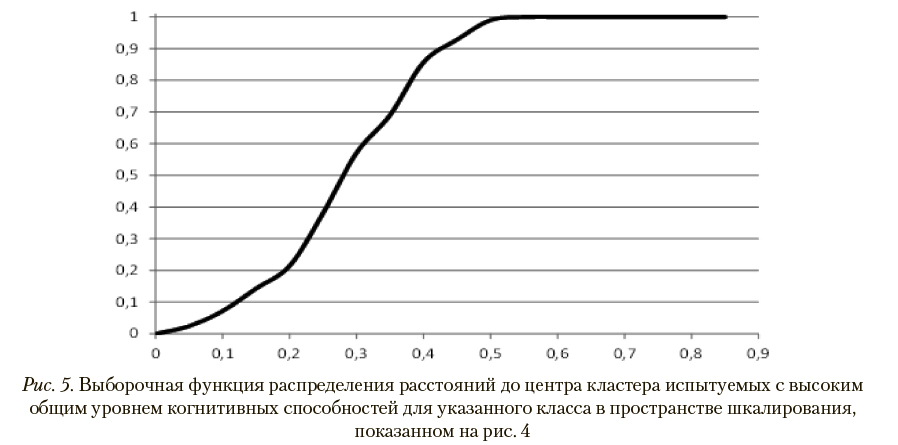
В наихудшем случае (при минимальном расстоянии до центра «чужого» кластера) для испытуемого с высоким общим уровнем когнитивных способностей вероятностные оценки корректной и некорректной классификации, вычисленные по расстояниям до центров кластеров с помощью указанных выборочных функций распределений, как указано в описании шага 7 метода паттернов в разделе 2, составляют, соответственно, 0,21 и 0,02. В случае испытуемого с низким общим уровнем когнитивных способностей аналогичные показатели равны 0,47 и значению, меньшему чем 0,01. Таким образом, при используемых параметрах диагностической процедуры обеспечивается 100% корректность распознавания классов.
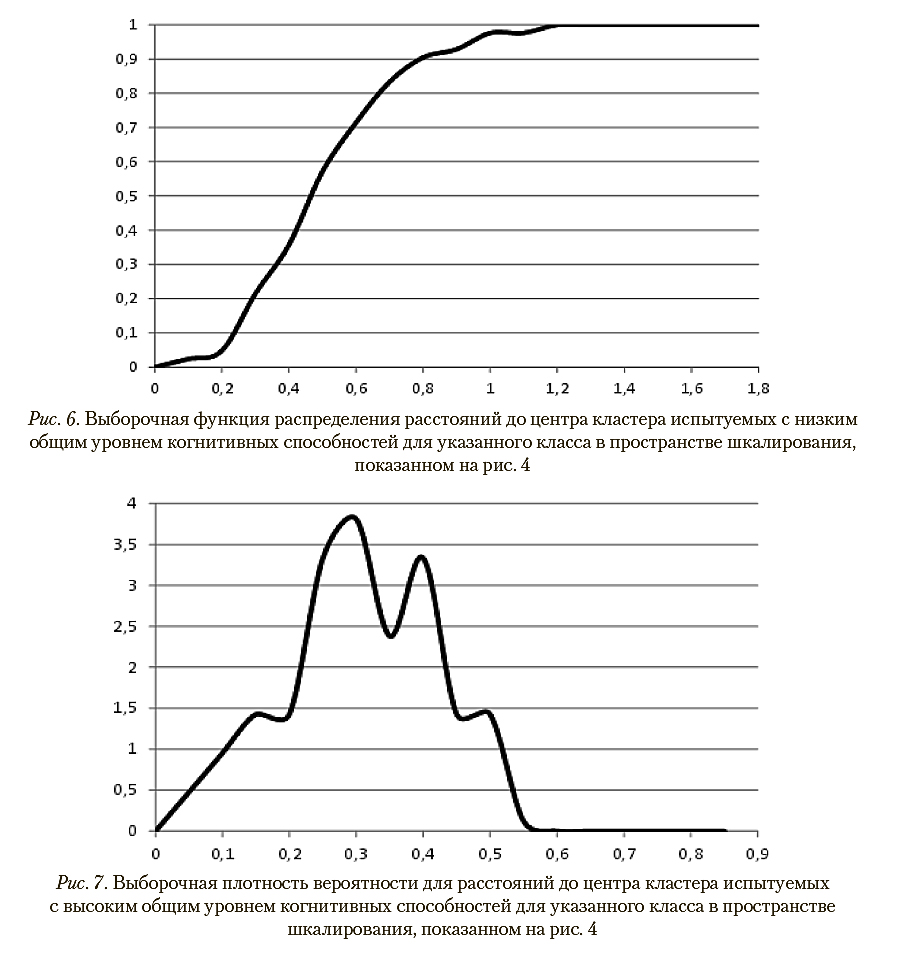
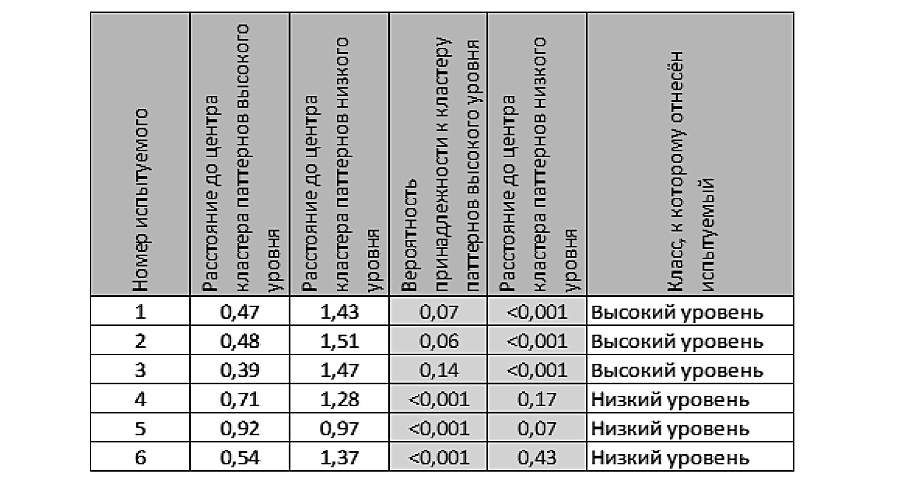
Для иллюстрации вычислений, выполняемых на шаге 7 метода паттернов, в табл. 2 приведены вероятностные оценки распознавания классов, к которым относятся 6 испытуемых, представленных маркерами в пространстве шкалирования на рис. 4. Эти оценки получены с помощью выборочных функций распределений, показанных на рис. 5 и 6.
Уменьшение в 2 раза количества заданий по каждому субтесту приводит к диаграмме рассеяния, представленной на рис. 9, и ухудшает указанные выше соотношения вероятностных оценок для наихудшего случая, соответственно, до 0,22/0,4 и 0,55/0,01, а корректность распознавания классов — до 97%. В целом, это свидетельствует о возможности уменьшения количества тестовых заданий за счет адаптации тестовых траекторий к результатам конкретных испытуемых.
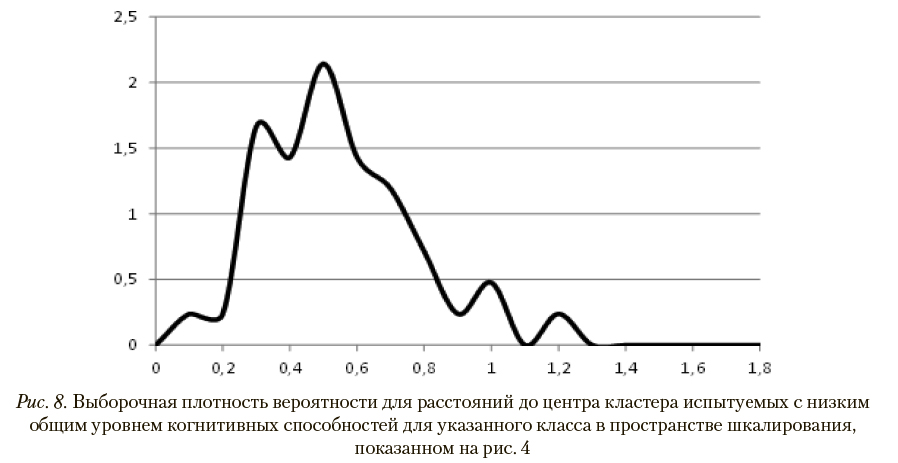
Таблица 2
Вероятностные оценки распознавания классов, к которым относятся 6 испытуемых, представленных на рис. 4
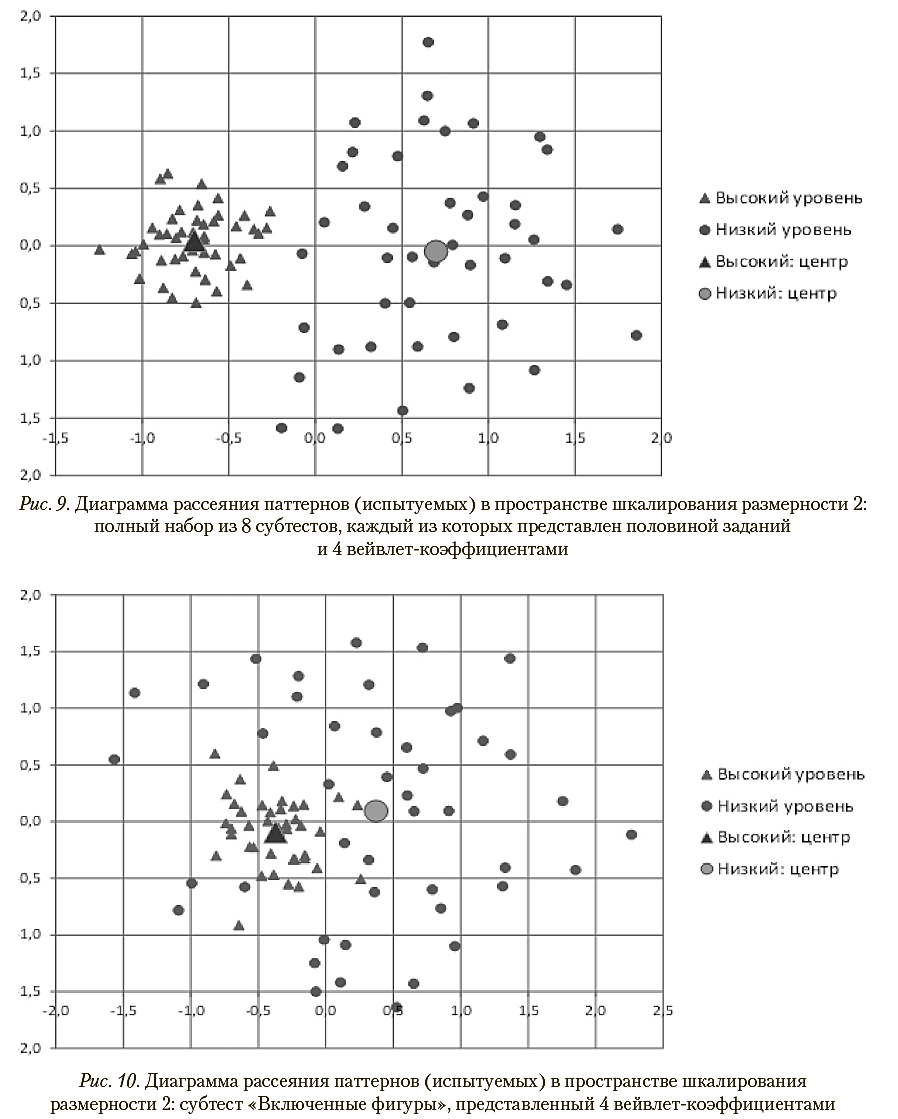
Использование рассмотренных выше вероятностных оценок при распознавании классов по отдельным субтестам приводит к существенному числу ошибок, что качественно иллюстрируется диаграммами рассеяния на рис. 10 и 11.
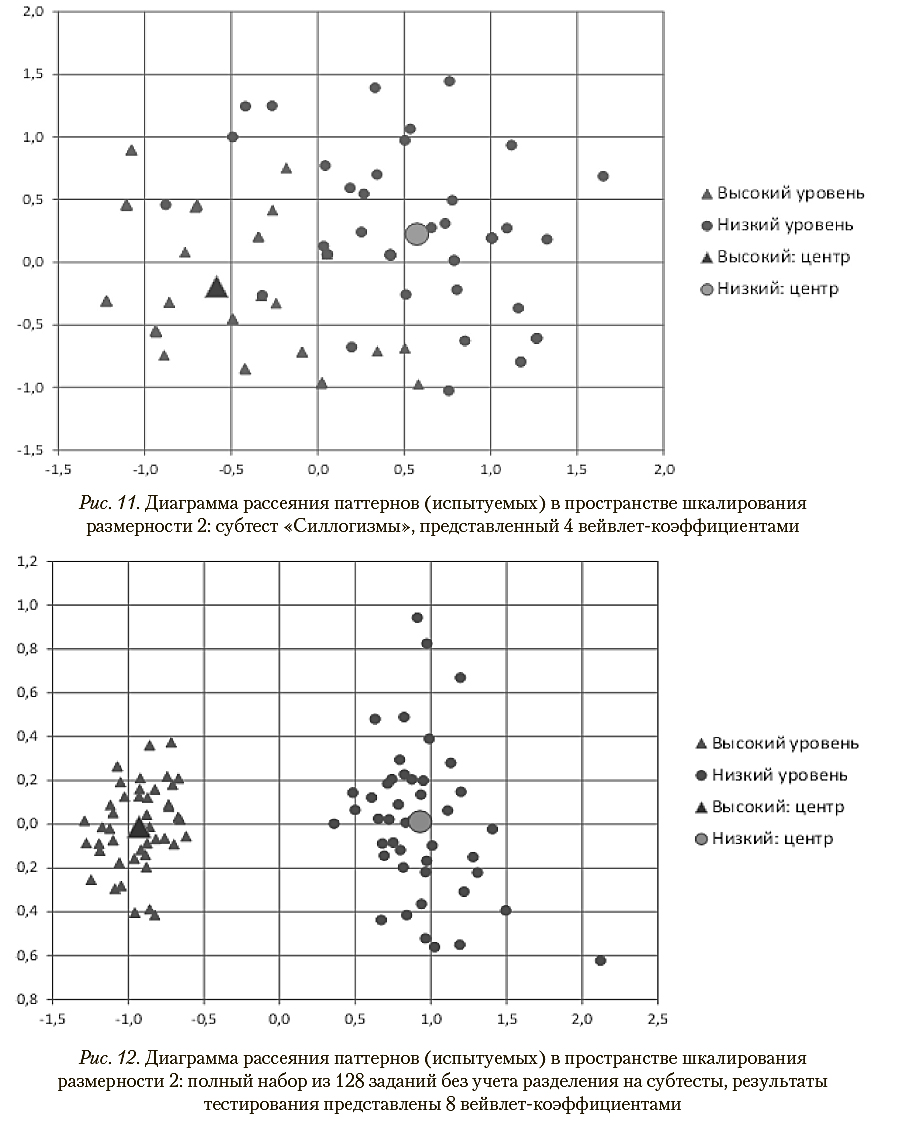
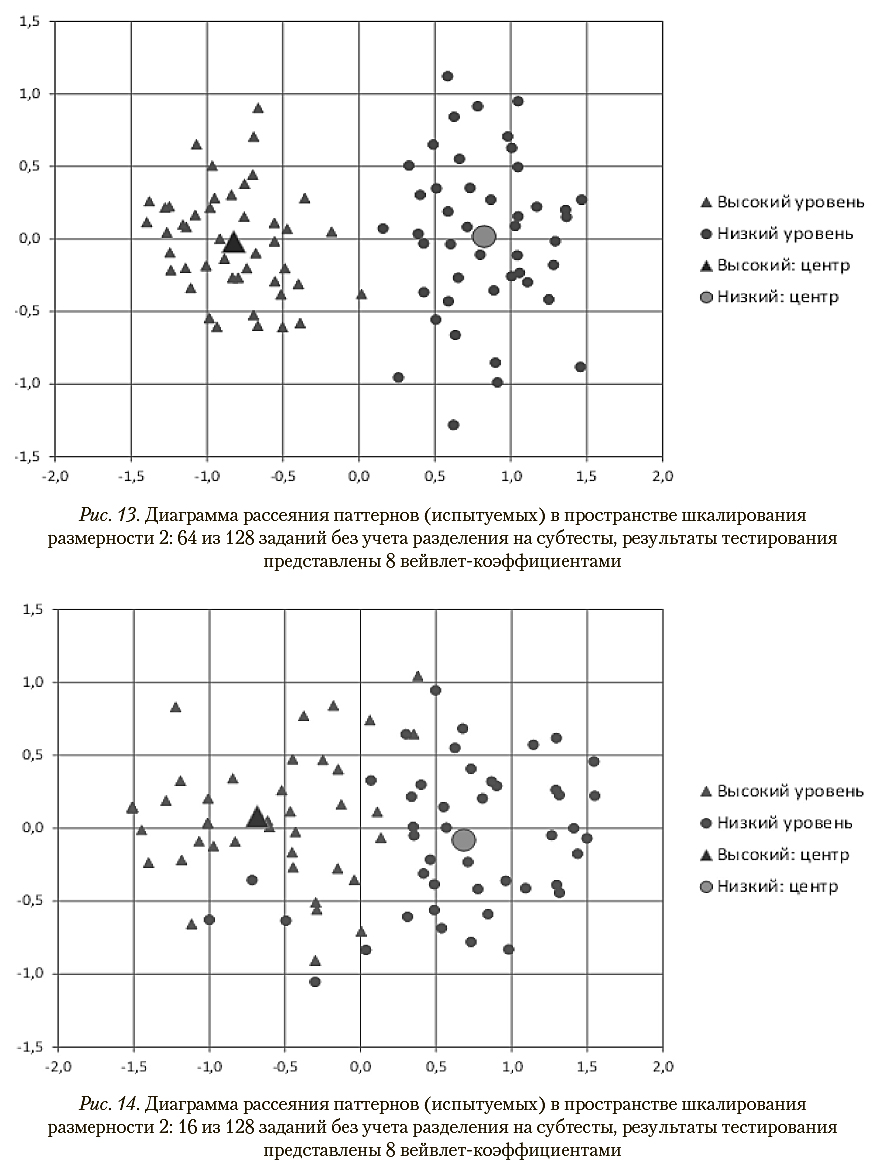
Анализ результатов тестирования без учета разделения на субтесты свидетельствует о возможности значительного сокращения числа тестовых заданий с приемлемым снижением надежности: в частности, использование для диагностики первых 64 вместо имеющихся 128 заданий приводит к снижению корректности распознавания классов со 100% до 88%. Этот вывод иллюстрируется диаграммами рассеяния, представленными на рис. 12—14.
Основные выводы и результаты
1. Разработан метод паттернов для диагностики испытуемых по тестовым траекториям — последовательностям значений, представляющим результаты выполнения тестовых заданий в порядке их появления.
2. Предложенный подход позволяет:
— решать задачи диагностики, располагая ограниченными результатами наблюдений;
— строить диагностические выводы, опираясь только на анализ эмпирических данных, накопленных к контрольному моменту времени;
— применять диагностическую процедуру, которая не имеет параметров, требующих настройки по репрезентативным экспериментальным данным.
3. В отличие от традиционных методов данный подход:
— учитывает динамику результативности выполнения тестовых заданий;
— работает с диагностическими характеристиками, непрерывно зависящими от времени (что, как правило, имеет место при диагностике операторов сложных технических систем);
— обеспечивает построение адаптивных технологий тестирования, позволяющих, в зависимости от результатов конкретного испытуемого, изменять как количество предъявляемых тестовых заданий, так и их содержание, добиваясь заданного уровня надежности диагностической оценки.
Финансирование
Работа выполнена при поддержке Российского фонда фундаментальных исследований (проект № 1729-07034).
1 В русскоязычной литературе также используются различные варианты ее названия: теория ответов на вопросы, стохастическая теория тестов, математическая теория измерений, современная теория тестирования, теория латентных черт, теория характеристических кривых заданий, теория моделирования и параметризации педагогических тестов и т. д.
Литература
- Валуева Е.А., Ушаков Д.В. Эмпирическая верификация модели соотношения предметных и эмоциональных способностей // Психология. Журнал Высшей школы экономики, 2010. Т. 7, № 2. С. 103—114.
- Куравский Л.С., Артеменков С.Л., Юрьев Г.А., Григоренко Е.Л. Новый подход к компьютеризированному адаптивному тестированию // Экспериментальная психология. 2017. Т. 10. №. 3. С. 33—45. doi:10.17759/exppsy.2017100303
- Куравский Л.С., Марголис А.А., Мармалюк П.А., Юрьев Г.А., Думин П.Н. Обучаемые марковские модели в задачах оптимизации порядка предъявления психологических тестов // Нейрокомпьютеры: разработка и применение. 2013. № 4. С. 28—38.
- Куравский Л.С., Марголис А.А., Мармалюк П.А., Панфилова А.С., Юрьев Г.А. Математические аспекты концепции адаптивного тренажера // Психологическая наука и образование. 2016. Т. 21. № 2. C. 84—95. doi: 10.17759/pse.2016210210
- Куравский Л.С., Марголис А.А., Юрьев Г.А., Мармалюк П.А. Концепция системы поддержки принятия решений для психологического тестирования // Психологическая наука и образование. 2012. № 1. С. 56—65.
- Куравский Л.С., Юрьев Г.А. Адаптивное тестирование как марковский процесс: модели и их идентификация // Нейрокомпьютеры: разработка и применение. 2011. № 2. С. 21—29.
- Куравский Л.С., Юрьев Г.А. Вероятностный метод фильтрации артефактов при адаптивном тестировании // Экспериментальная психология. 2012. Т. 5. № 1. С 119—131.
- Куравский Л.С., Юрьев Г.А. Использование марковских моделей при обработке результатов тестирования // Вопросы психологии. 2011. № 2. С. 98—107.
- Куравский Л.С., Юрьев Г.А. Об одном подходе к адаптивному тестированию и устранению его артефактов // Нейрокомпьютеры: разработка и применение. 2012. № 1.
- Марковские модели в задачах диагностики и прогнозирования: учеб. пособие / Под ред. Л.С. Куравского. 2-е изд., доп. М.: Изд-во МГППУ, 2017. 203 с.
- Baker F.B. The Basics of Item Response Theory. ERIC Clearinghouse on Assessment and Evaluation, University of Maryland, College Park, MD, 2001.
- Borg I., Groenen P.J.F. Modern Multidimensional Scaling Theory and Applications // Springer. 2005. P. 140.
- Gregory R.J. Psychological testing: History, principles, and applications (5th edition). New York: Pearson, 2007.
- Gulliksen H. Theory of Mental Tests. John Wiley & Sons Inc, 1950.
- Kuravsky L.S., Marmalyuk P.A., Baranov S.N., Alkhimov V.I., Yuryev G.A. and Artyukhina S.V. A New Technique for Testing Professional Skills and Competencies and Examples of its Practical Applications // Applied Mathematical Sciences. 2015. Vol. 9. № 21. Р. 1003—1026, https://doi.org/10.12988/ ams.2015.411899
- Kuravsky L.S., Marmalyuk P.A., Yuryev G.A. and Dumin P.N. A Numerical Technique for the Identification of Discrete-State Continuous-Time Markov Models [Электронный ресурс] // Applied Mathematical Sciences. 2015. Vol. 9. № 8. Р. 379—391. URL: https://doi.org/10.12988/ams. 2015.410882 (дата обращения: 16.06.2018)
- Neal Phillip Grieb. Multiresolution Analysis for Adaptive Refinement of Multiphase Flow Computations. University of Iowa, 2010. P. 116.
- Rasch G. Probabilistic models for some intelligence and attainment tests // Copenhagen, Danish Institute for Educational Research, expanded edition (1980) with foreword and afterword by B.D. Wright. Chicago: The University of Chicago Press. 1960/1980.
- René Vidal, Yi Ma, Shankar Sastry. Generalized Principal Component Analysis [Электронный ресурс] // Springer-Verlag New York, 2016. URL: http://www.springer.com/ us/book/9780387878102 (дата обращения: 16.06.2018)
- Thompson N.A., Weiss D.J. A framework for the development of computerized adaptive tests // Practical Assessment, Research & Evaluation, 2011. 16(1), З. 1—9.
- Torre J. de la, Patz R.J. Making the Most of What We Have: A Practical Application of Multidimensional Item Response Theory in Test Scoring // Journal of Educational and Behavioral Statistics. 2005. 30(3) Р. 295—311. doi:10.3102/10769986030003295.
- Trevor F. Cox, M.A.A. Cox. Multidimensional Scaling, Second Edition. Chapman & Hall/CRC, 2001. P. 299.
- Wright B.D., Masters G.N. Rating scale analysis. Rasch measurements. Chicago: MESA Press, 1982.
- Xiangyu Kong, Changhua Hu, Zhansheng Duan. Principal Component Analysis Networks and Algorithms [Электронный ресурс] // Springer, 2017. URL: http://www.springer.com/us/book/9789811029134 (дата обращения: 16.06.2018)
- Young F. MDS: History, Theory, and Applications. Psychology Press, 2013. P. 317.
Информация об авторах
Метрики
Просмотров web
За все время: 1704
В прошлом месяце: 25
В текущем месяце: 11
Скачиваний PDF
За все время: 758
В прошлом месяце: 4
В текущем месяце: 6
Всего
За все время: 2462
В прошлом месяце: 29
В текущем месяце: 17