Экспериментальная психология
2016. Том 9. № 3. С. 27–40
doi:10.17759/exppsy.2016090303
ISSN: 2072-7593 / 2311-7036 (online)
Зависимость иллюзии Оппель-Кундта от конфигурации составляющих линий
Аннотация
Общая информация
Ключевые слова: геометрические иллюзии, иллюзия Оппель–Кундта, оценка размера, пространственно-частотный анализ, модель модулей
Рубрика издания: Психология восприятия
Тип материала: научная статья
DOI: https://doi.org/10.17759/exppsy.2016090303
Для цитаты: Бондарко В.М., Бондарко Д.В., Чихман В.Н. Зависимость иллюзии Оппель-Кундта от конфигурации составляющих линий // Экспериментальная психология. 2016. Том 9. № 3. С. 27–40. DOI: 10.17759/exppsy.2016090303
Полный текст
БОНДАРКО В. М. , Институт физиологии имени И.П. Павлова РАН, Санкт-Петербург, Россия, e-mail: vmbond@gmail.com
БОНДАРКО Д. В.[*] [†], Институт физиологии имени И.П. Павлова РАН, Санкт-Петербург, Россия, e-mail: dmvb8@mail.ru
ЧИХМАН В. Н.[‡], Институт физиологии имени И.П. Павлова РАН, Санкт-Петербург, Россия, e-mail: niv@pavlov.infran.ru
Исследовали различение размеров пространственных интервалов, ограниченных двумя прямыми или изогнутыми линиями. Размеры интервалов варьировали от 2,56 до 3,12 угл. град. Задача наблюдателя заключалась в оценке расстояния между линиями. Проведено три эксперимента. В первом эксперименте дополнительные прямые линии разделяли интервал на равные промежутки; таким образом, мы исследовали иллюзию Оппель-Кундта. Была получена инвариантная по отношению к размеру интервала зависимость величины иллюзии от числа линий. Во втором эксперименте размер пространственного интервала оценивался в случае присутствия двух дополнительных линий, расположенных внутри интервала на различных расстояниях. Максимальная по величине иллюзия возникала при одинаковом расстоянии между линиями. В третьем эксперименте между двумя изогнутыми параллельными линиями на равном расстоянии могли находиться еще две такие же линии. Полученная здесь иллюзия была по величине больше иллюзии для интервалов, ограниченных отрезками прямых линий. Модель модулей дала хорошую аппроксимацию данных по изучению иллюзии Оп- пель-Кундта.
Существует большое количество экспериментальных данных по оценке размеров изображений. Тем не менее, проблему оценки размера продолжают изучать и получают все новые и новые результаты, которые свидетельствуют о сложности проблемы. Так, с оценкой размера зрительных изображений связано наибольшее количество зрительных иллюзий. Это такие известные иллюзии, как иллюзия Луны, Мюллера-Лайера, Титченера, Эббинхауза, Оппель-Кундта и другие. В настоящем исследовании мы остановимся подробно на изучении иллюзии Оппель-Кундта (ОК). Эта иллюзия заключается в том, что заполненный параллельными линиями пространственный интервал кажется более протяженным, чем интервал, ограниченный только двумя параллельными линиями по краям.
Иллюзия Оппель-Кундта отличается большим разнообразием в зависимости от числа заполняющих промежуток линий и размера промежутка. В большинстве известных исследований при увеличении числа линий величина иллюзии сначала увеличивается, затем достигает максимума, а в дальнейшем постепенно уменьшается (Coren, Girgus, 1978). Максимум приходится примерно на 6-15 заполняющих промежуток линий. Нужно отметить, что при нахождении максимума наблюдается большой разброс, зависящий от условий предъявления и характеристик стимулов.
В работе Булатова, Бертулиса и Мицкене (Bulatov, Bertulis, Mickene, 1997) было показано, что иллюзия ОК практически инвариантна по отношению к величине промежутка для 10 линий, но не выявлено четкой зависимости от числа линий (большой разброс у одного из двух принимавших участие в исследовании наблюдателей затруднил нахождение максимума, а аппроксимация данных двух наблюдателей выявила различные максимумы), хотя авторы пишут, что максимум наблюдается при 6-15 линиях. Ротвел и Зайдел (Rothwell, Zajdel, 1990) не нашли значимого различия в иллюзии при четырех и девяти линиях. У Крейнера (Kreiner, 2009) в зависимости от количества линий максимум сдвигался в большую сторону (от 5 до 11 линий) при увеличении размера пространственного интервала. Вакерман и Кастнер (Wackermann, Kastner, 2010) получили максимальный эффект для 11-13 линий. У Гиора и Гори (Giora, Gori, 2010) при использовании в качестве изображений шахматных досок иллюзия была сильнее для доски из 8х8 квадратов по сравнению с доской из 16х16 квадратов. Таким образом, не выявлено однозначной закономерности изменения иллюзии ОК от количества линий.
Чаще всего иллюзия Оппель-Кундта интерпретируется как константность восприятия размера (например, Kreiner, 2009). Гипотеза о возможном применении механизма константности размера первоначально была предложена Грегори (Gregory, 1963; Грегори, 1970) для объяснения таких иллюзий размера, как иллюзия Мюллера-Лайера и Понцо. Предполагается, что в изображениях фигур, вызывающих эти иллюзии, присутствуют признаки перспективы, которые приводят к тому, что одни части рисунка воспринимаются более близкими, а другие более далекими. Если проекции двух объектов на сетчатке одинаковы, а воспринимаемая удаленность объектов различается, то размер дальнего объекта кажется больше, чем размер ближнего. Иллюзия Понцо может рассматриваться как двумерная проекция трехмерной сцены, в которой наклонные линии являются зрительными признаками перспективы. Подобным образом можно объяснить и иллюзию Оппель-Кундта. Крейнер (Kreiner, 2009) предположил, что зрительная система концентрируется на оценке узких промежутков, которые могут казаться более удаленными, чем широкие промежутки. Это, в свою очередь, приводит к увеличению воспринимаемого размера, примерно пропорционально числу линий. При дальнейшем увеличении плотности линий зрительная система воспринимает их не по отдельности, а как нечто целое, как однородный паттерн. В результате величина иллюзии уменьшается. В своем предположении Крейнер опирается на свои данные об оценке размера в зависимости от расстояния до объекта: при увеличении расстояния воспринимаемый размер объекта увеличивается при пропорциональном к расстоянию размере на сетчатке. Следует отметить, что последнее утверждение является спорным. Многие исследователи полагают, что размер оценивается пропорционально расстоянию (Foley, Ribeiro-Filho, Da Silva, 2004; Gogel, 1971; Higashiyama, Adachi, 2006). Поэтому такое объяснение трудно считать удовлетворительным.
А.Н. Булатов, А.В. Бертулис и Л.И. Мицкене (1995) сделали попытку подойти к решению проблемы возникновения геометрических иллюзий с точки зрения функционирования отдельных нейронов зрительной системы. Авторы предположили, что иллюзии определяются главным образом свойствами пространственно-частотной (ПЧ) фильтрации на уровне первичной зрительной коры. При оценке размера сопоставляются отфильтрованные изображения сравниваемых стимулов. Стимул кажется большим по размеру при большей области, занимаемой отфильтрованным изображением. При изучении иллюзии Опель-Кундта и Мюллера-Лайера эти исследователи (Bulatov, Bertulis, Mickene, 1997) выявили существенные индивидуальные различия, которые объяснили разной стратегией (один наблюдатель больше обращает внимание на правый стимул, другой - на левый) и различиями у них в пространственно-частотных характеристиках (ПЧХ). ПЧХ человека имеет максимум на частотах 2-4 цикла на градус в зависимости от условий освещенности. Согласно их модели, увеличение размера интервала должно приводить к сдвигу максимума иллюзии в сторону большего количества линий, как это и наблюдал Крейнер (Kreiner, 2009). Но экспериментов по оценке иллюзии в зависимости от величины интервала, как и измерение ПЧХ наблюдателей, эти исследователи не проводили.
Близкую интерпретацию иллюзии ОК дают Гиора и Гори (Giora, Gori, 2010) при использовании в качестве стимулов шахматных досок с регулярным и случайным расположением черных квадратов. Они показали, что иллюзия зависит от ПЧХ изображений и ее величина уменьшается при случайном расположении квадратов. Авторы объясняют это тем, что рецептивные поля первичной зрительной коры имеют ориентационную настройку. При случайном расположении квадратов у паттерна ориентационная составляющая уменьшается, что приводит к уменьшению величины иллюзии.
В ряде работ (Бондарко, Данилова, 1998; Bondarko, Danilova, 1999; Hess, Badcock, 1995) показано, что на оценку величины пространственного интервала влияют дополнительные изображения, расположенные снаружи интервала, как правило, в сторону увеличения ширины пространственного интервала. Проявляется влияние дополнительных контуров, которое можно объяснить как их ассимиляцией с линиями, задающими интервал, так и взаимодействием между ПЧ-каналами. Нейрофизиологической основой такого взаимодействия могут служить механизмы изо- и кросс-ориентационного торможения между нейронами стриарной коры (Kisvarday et al., 1994). Тип торможения изменяется в зависимости от расстояния между клетками, в которые приходит сигнал. Взаимодействие между ПЧ-каналами, полученное в психофизических экспериментах, проявляется как торможение при близком расстоянии между центральным стимулом и окружением и как растормаживание при больших расстояниях (Polat, Sagi, 1993). Возможно, что подобными взаимодействиями можно объяснить и иллюзию ОК. Экспериментальных исследований по оценке размера интервалов с добавочными линиями внутри интервала проведено не было.
Для проверки высказанных выше предположений в настоящем исследовании мы попытались определить максимум величины иллюзии в зависимости от числа линий при изменении величины пространственного интервала. Кроме того, попытались оценить величину пространственного интервала при добавлении к нему линий, находящихся внутри интервала в случае прямых и изогнутых линий. Такой дополнительный экспериментальный материал, с нашей точки зрения, позволит определить вклад в возникновение иллюзии ОК механизма взаимодействия между контурами и ПЧ-анализа. Кроме того, в работе сделана попытка промоделировать полученную зависимость иллюзии ОК от числа линий с использованием частного случая ПЧ-анализа изображений, так называемой моделью модулей (Глезер, 1985).
Методика
Аппаратура. Стимулы были синтезированы на мониторе Mitsubishi Diamond Plus 230SB с размером диагонали 22” при разрешении экрана 1024х768 пикселей и частотой вертикальной развертки 100 Гц. Калибровка монитора выполнялась с помощью спектроради- ометра JETI.
Стимулы. Пространственные интервалы задавались двумя параллельными вертикальными линиями. Толщина линий была равна 0,8 угл. мин., длина - 2,5 угл. град. Предъявляли темные линии (5 кд/м2) на светлом фоне (40 кд/м2). Тестовые изображения представляли собой пространственные интервалы, ограниченные либо двумя вертикальными прямыми линиями, либо двумя изогнутыми линиями, образованными половинами окружностей. У тестовых изображений менялось расстояние между линиями. У референтных стимулов расстояние между двумя крайними линиями было фиксированным, равным 1,56; 1,95; 2,34; 2,73 или 3,12 угл. град. Внутри крайних линий, задающих величину пространственного интервала, могли находиться линии той же формы, но на различном расстоянии от крайних линий.
Было проведено три эксперимента, отличающихся стимулами. В первом эксперименте пространственный интервал был ограничен отрезками прямых линий, между которыми на равном расстоянии могли располагаться 1, 2, 5, 9 или 14 линий, т. е. референтный стимул состоял из 2, 3 4, 7, 11 и 16 линий. Во втором эксперименте между двумя крайними линиями, образующими пространственный интервал, находились две линии на расстояниях, равных 1/9, 2/9, 3/9 или 4/9 величины интервала. При расстоянии 3/9 изображение совпадало с изображением, состоящим из четырех линий в эксперименте 1 (две линии внутри промежутка). В третьем эксперименте интервал был ограничен изогнутыми линиями, образованными полуокружностями. Референтный интервал был ограничен либо двумя линиями, либо внутри на одинаковом расстоянии находилось еще две изогнутые линии. Примеры изображений, использованных в трех экспериментах, показаны на рис. 1.
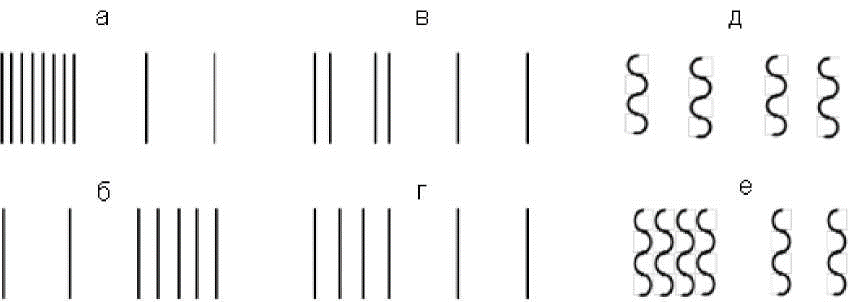
Рис. 1. Примеры изображений, использованных в исследовании:
a, б - изображения стимулов первого эксперимента; в, г - второго; д, е - третьего; a - слева показан референтный стимул, состоящий из 8 линий, справа - тестовый; б - слева - тестовый стимул, справа - референтный из 5 линий; в - слева - референтный стимул из 4 линий, справа - тестовый; г - слева - референтный стимул из 4 равноотстоящих линий, справа - тестовый; д, е - стимулы из изогнутых линий
Процедура. Для оценки величины пространственных интервалов использовали методы вынужденного выбора и константных стимулов. На экране одновременно случайным образом справа или слева предъявляли тестовый и референтный стимулы. Расстояние между краями стимулов было равно 2,5 угл. град. Наблюдатель должен был ответить, справа или слева изображен больший по размеру интервал. Ответ «не знаю» разрешен не был. Для каждого референтного стимула было взято 9 тестовых интервалов, величина которых менялась с определенным в предварительных экспериментах шагом. Шаг изменения величины интервала подбирался для каждого наблюдателя таким образом, чтобы вероятность ответа «больше» находилась в диапазоне 0,2-0,8. Тестовые и референтные изображения предъявляли одновременно справа и слева относительно центра экрана случайным образом, чтобы избежать возможного часто наблюдаемого преувеличения размера стимула в правом или левом полуполе зрения.
В одной серии фиксировали расстояние между крайними линиями у референтного стимула. В следующей серии размер референтного стимула был другим. Серии с различными размерами интервалов у референтных стимулов чередовали случайным образом и проводили в один день. Данные, полученные в разные экспериментальные дни, суммировали. Всего каждую пару стимулов (тестовый с различной величиной + референтный) при различном расстоянии до боковых линий предъявляли 50 раз. При предъявлении стимулы сдвигались вправо или влево относительно центра экрана случайным образом в пределах 20 угл. мин. Точка фиксации не использовалась. Наблюдение было бинокулярным с расстояния 170 см до экрана.
Анализ данных. Для определения порогов для каждого испытуемого были построены суммарные психометрические функции для ответов «больше» по всем экспериментам при каждом референтном стимуле. Для определения порогов был использован пробит-анализ. С помощью метода наименьших квадратов психометрические функции были приближены к функциям нормального распределения. Разницы между экспериментальными данными и полученными нормальными распределениями были оценены по методу %2.
Пороги различения величины пространственных интервалов вычисляли как стандартные отклонения полученных нормальных распределений, что соответствует значению порогов на уровне 84% правильных ответов на психометрической функции. Величины средних значений у нормальных распределений соответствуют тем размерам, при которых наблюдатели считают референтные стимулы равными тестовым - так называемые точки субъективного равенства. В нашем исследовании средние значения распределений сравниваются с физическими размерами интервалов и используются для оценки искажения восприятия величины интервалов: из средних значений вычитаются физические размеры.
Наблюдатели. В экспериментах приняли участие четыре наблюдателя с нормальной или скорректированной остротой зрения. Все наблюдатели имели опыт участия в психофизических экспериментах, но не были осведомлены о целях данного исследования.
Исследование было одобрено Этическим комитетом СПбГУ.
Результаты
Эксперимент 1. Полученные психометрические функции были приближены к нормальным распределениям и эти приближения оказались довольно точными (p<0,01 для всех кривых). На рис. 2 показаны усредненные по данным четырех наблюдателей результаты первого эксперимента. Величины среднеквадратичного отклонения (сигмы) были взяты в качестве порогов различения величины интервалов. На рис. 2-а показаны зависимости изменения порогов от количества линий в референтном стимуле в первом эксперименте. Отдельные кривые (1-5) приведены для пространственных интервалов величиной в 1,56; 1,95; 2,34; 2,73 или 3,12 угл. град. Взяты относительные к величине пространственных интервалов пороги, так называемые фракции Вебера-Фехнера. Величины порогов оказались немного выше для 3, 4 и 7 полос по сравнению с порогами различения величины интервала, не имеющего линий внутри. Двухфакторный (размер интервала, разные референтные стимулы) дисперсионный анализ (ANOVA) показал достоверные различия порогов в зависимости от этих факторов (F[Булатов, 1995]= 3,59; p=0,023; F[Глезер, 1985]= 8,21, p=0,002). Попарное сравнение порогов в случае стимулов из двух и трех, двух и четырех или двух и семи линий выявило достоверные их различия по критерию Стьюдента (t1= 6,04; t2 = 2,4834; t3 = 2,12935; p<0,05). То есть пороги различения интервалов достоверно выше при добавлении линий в этих случаях.
На рис. 2-б приведены разности между средними величинами полученных нормальных распределений и физическими размерами стимулов в зависимости от количества линий в референтных стимулах, отражающие величину возникшей иллюзии. Разности выражены в процентах по отношению к размеру стимула. Кривые 1, 2, 3, 4, 5 соответствуют величине пространственных интервалов в 1,56; 1,95; 2,34; 2,73 или 3,12 угл. град. Для пространственных интервалов, состоящих из двух линий и не имеющих внутри дополнительных линий, эти разности колеблются около нуля, в то время как для пространственных интервалов с разделительными линиями возникает иллюзия. Величина пространственных интервалов переоценивается на 5-15% в зависимости от количества линий. Максимальная иллюзия возникает при 7 линиях в референтном стимуле независимо от величины пространственного интервала. Сначала по мере увеличения числа линий иллюзия возрастает, затем падает. Немного меньшие по величине иллюзии возникают для более широких пространственных интервалов. Двухфакторный дисперсионный анализ не выявил различий в иллюзии в зависимости от величины пространственного интервала (F[Булатов, 1995]=2,92; p=0,054), но показал сильную зависимость от числа линий в стимулах (F[Глезер, 1985]= 145,97; p<0,0001). Таким образом, иллюзия оказалась инвариантна по отношению к величине пространственных интервалов.
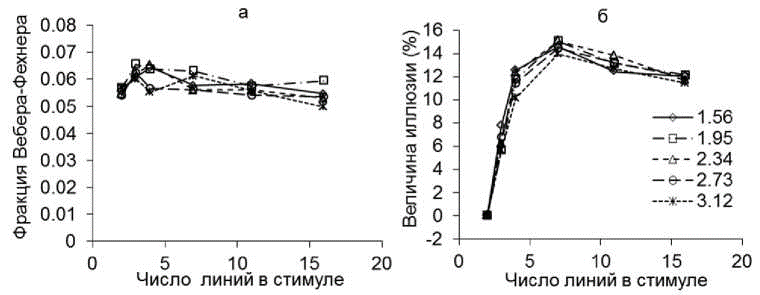
Рис. 2. Различение величины интервала в зависимости от числа линий в стимуле: a - относительные пороги различения величины интервала. Ось абсцисс - число линий в референтном стимуле. Ось ординат - фракции Вебера-Фехнера в отн. ед. б - величина иллюзии в процентном выражении по отношению к величине референтного интервала. Отдельные кривые соответствуют размерам референтных стимулов от 1,5 до 3,2 угл. град.
Эксперимент 2. На рис. 3 приведены результаты второго эксперимента, где референтными стимулами служили либо интервалы без дополнительных линий, либо интервалы, внутри которых на разных расстояниях могли находиться две дополнительные линии. На рис. 3-а приведены пороги различения величины интервала в зависимости от расстояния до двух дополнительных линий. Пороги несколько выше в случае присутствия дополнительных линий, в среднем в 1,2 раза, и практически не зависят от расстояния между линиями. Двухфакторный дисперсионный анализ (размер интервала, разные расстояния между линиями) показал недостоверные различия порогов от размера интервала (F[Булатов, 1995]= 2,21; p=0,126) и достоверные от наличия дополнительных линий в стимуле (F[Булатов, 1995]= 15,08; p<0,001).
На рис. 3-б показана величина возникающей иллюзии в зависимости от расстояния до дополнительных линий в процентах по отношению к величине интервала. Отдельные кривые даны для разных по величине пространственных интервалов. При расстоянии, равном нулю, референтный пространственный интервал не имеет дополнительных линий. Сила иллюзии увеличивается практически пропорционально расстоянию между линиями в стимуле до расстояния, равного 3/9=1/3, а затем величина иллюзии уменьшается. Максимальная величина иллюзии составляет 13,5%. Величина иллюзии меньше для больших пространственных интервалов, эти различия достоверны (диперсионный анализ по факторам размер интервала, расстояние до линий: F[Булатов, 1995]= 49,55; F[Булатов, 1995]= 179,46; p<0,000001). При расстоянии, равном 3/9=1/3, линии расположены на одинаковом расстоянии друг от друга. Референтный стимул в этом случае совпадает со стимулом, использованным в первом эксперименте и состоящим из четырех линий. Величина иллюзии практически совпадает в первом и втором экспериментах для больших интервалов (рис. 4-б).
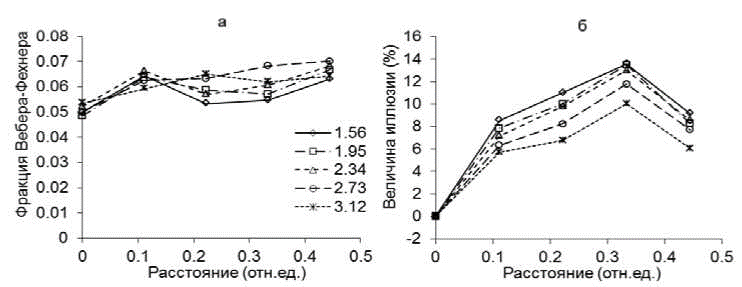
Рис. 3. Различение величины интервала в зависимости от расстояния до дополнительных линий в стимуле: a - относительные пороги различения величины интервала. Ось абсцисс - расстояние до линий в референтном стимуле в относительных единицах к величине интервала. Ось ординат - фракции Вебера-Фехнера. б - величина иллюзии в процентном выражении по отношению к ширине референтного интервала
Эксперимент 3. На рис. 4 показаны результаты третьего эксперимента с использованием изогнутых линий, ограничивающих величину пространственного промежутка. В референтном стимуле дополнительные изогнутые линии находились на равном расстоянии друг от друга и от основных линий (рис. 1-д, е). Здесь на рис. 4-а показаны пороги различения ширины интервала в зависимости от величины пространственного промежутка (кривые 1, 2 для изогнутых линий), а на рис. 4-б - величина иллюзии. Данные сравниваются с аналогичными результатами первого и второго экспериментов (данные с четырьмя равноотстоящими линиями). Фракции Вебера-Фехнера показаны отдельно для различения размера стимулов из двух и из четырех линий. Пороги не зависят от величины интервала во всех случаях. Но пороги выше для интервалов, образованных изогнутыми линиями, по сравнению с порогами в первом и втором экспериментах для интервалов из прямых линий. Кроме того, пороги выше в случае присутствия дополнительных линий в каждом из экспериментов. Ниже всего оказались пороги, полученные во втором эксперименте. На рис. 4-б во всех трех экспериментах иллюзия уменьшается при увеличении величины интервала. По сравнению с иллюзиями, возникающими при минимальной ширине интервала, иллюзии в 1,24; 1,35 и в 1,3 раза меньше для самого широкого интервала в первом, втором и третьем экспериментах соответственно.
В качестве дополнительного анализа при использовании интервалов, образованных изогнутыми линиями, мы провели двухфакторный дисперсионный анализ для исследования зависимости иллюзии от величины интервала (четыре степени свободы) и разных наблюдателей (три степени свободы). Оба эти фактора оказались значимыми, в большей степени оказала влияние величина интервала. Дисперсионный анализ для величины иллюзии в зависимости от размера дал следующее значение распределения Фишера: F[Булатов, 1995]= 15,4 (p<0,001). Таким образом, для интервалов, образованных изогнутыми линиями величина иллюзии зависит от величины пространственного интервала.
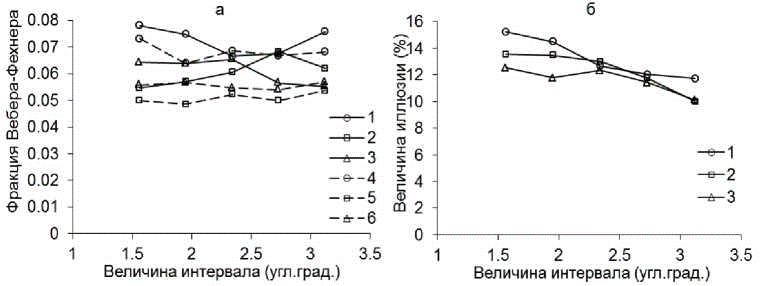
Рис. 4. Сравнение результатов трех экспериментов в зависимости от величины интервала: a - относительные пороги различения ширины интервала. Ось абсцисс - величина интервала. Ось ординат - фракции Вебера-Фехнера. Кривые 1, 2, 3 пороги для различения ширины стимулов, состоящих из четырех линий; 4, 5, 6 - из двух линий. Кривые 1, 4 - линии изогнуты; 2, 5 -прямые линии в эксперименте 2, 3, 6 - прямые линии в эксперименте 1. б - величина иллюзии. Ось абсцисс - величина интервала. Ось ординат - величина иллюзии в процентном выражении. Кривые 1, 2, 3 иллюзии для случаев изогнутых линий и прямых линий в экспериментах 2 и 1 соответственно
Обсуждение
Данная работа посвящена изучению иллюзии Оппель-Кундта. Мы наблюдали искажение в восприятии размера пространственных интервалов, ограниченных прямыми или изогнутыми линиями, при добавлении дополнительных линий. Результаты свидетельствуют о зависимости оценки размера от количества линий и расстояния между ними. В большинстве случаев присутствие добавочных линий приводит к увеличению порогов и всегда - к переоценке размера стимула.
В настоящей работе было проведено три разных эксперимента. Остановимся сначала на сравнении полученных в них данных.
Пороги различения размера оказались выше в третьем эксперименте для интервалов, образованных изогнутыми линиями, особенно по сравнению с порогами, полученными во втором эксперименте. Этот результат представляется естественным: легче различать размеры изображений простой формы (Бертулис, Булатов, Логинович, 1995). Уменьшение порогов во втором эксперименте по сравнению с первым может быть связано как с обучением, так и с тем, что во втором эксперименте использовалось немного меньшее количество референтных стимулов (пять вместо шести). В работе Глезера и др. (1997) было показано, что при увеличении набора референтных стимулов пороги возрастают.
Максимальная по абсолютному значению величина иллюзии при одном и том же количестве линий была получена в третьем эксперименте, где интервалы были ограничены изогнутыми линиями. Но разница в величине иллюзии для трех экспериментов не слишком велика (см. рис. 4-б), максимально для одних и тех же размеров величины иллюзии отличаются в 1,2 раза. Поэтому мы не можем утверждать с полной уверенностью, что действительно при использовании изогнутых линий величина иллюзии больше, поскольку эксперименты проводились последовательно, и за время их проведения могли меняться состояние наблюдателей и критерий оценки. Можно только заключить, что не подтверждается предположение Гиора и Гори (Giora, Gori, 2010) о том, что большую роль в возникновении иллюзии играет ориентационная составляющая, поскольку для изогнутых линий эта составляющая меньше, чем для прямых. Интересно сравнить иллюзии, полученные в первом и втором экспериментах. В первом эксперименте максимальные величины иллюзии наблюдались при 7 линиях, расстояние между которыми составляло 1/6=0,166 от размера стимула. Если бы величина иллюзии определялась расстоянием между ближайшими к краям интервала линиями, то во втором эксперименте максимум величины иллюзии должен был приходиться на относительное расстояние, равное 0,11 или 0,22. Максимум во втором эксперименте был получен при расстоянии 0,33, т. е. при равном разделении промежутка линиями. Таким образом, величина иллюзии больше для регулярно расположенных линий.
Мы показали, что величина иллюзии в процентном выражении уменьшается при увеличении ширины пространственных интервалов во всех трех экспериментах при добавлении двух дополнительных линий. Однако в первом эксперименте, в отличие от других экспериментов, мы не получили достоверного уменьшения иллюзии при увеличении ширины интервалов в случае предъявления разного числа линий. Это наглядно продемонстрировано на рис. 2-б - кривые зависимостей величины иллюзии от числа линий при разной величине интервалов пересекаются друг с другом, особенно для большого количества линий в стимуле. В первом эксперименте для разного числа линий максимальная величина иллюзии наблюдается при семи линиях в стимуле для всех величин пространственных интервалов. Подобная инвариантная по отношению к величине пространственных интервалов зависимость противоречит гипотезе, предложенной Булатовым, Бертулисом и Мецкене (1995), о возникновении иллюзии ОК за счет фильтрации изображений ПЧ-каналами с последующей оценкой размеров отфильтрованных изображений. Максимум величины иллюзии, согласно этой гипотезе, приходится на наиболее чувствительный ПЧ-канал, где период частоты равен расстоянию между соседними линиями. В рамках этих предположений, в нашем случае при увеличении величины промежутка в два раза максимум должен был сдвинуться в сторону большего количества линий. Однако этого не происходит.
Каким образом можно интерпретировать полученные нами данные?
Как и многие исследователи, мы предполагаем, что описание объектов в первом приближении может осуществляться конечным набором ПЧ-фильтров. Каждый объект оптимальным образом (с наименьшей потерей информации) описывается своим набором фильтров, заданных на определенном участке поля зрения. Объекты кажутся равными по размеру, если описывающие их фильтры заданы на областях одного размера. Этих положений придерживаются в своих исследованиях и Булатов с соавторами (Bulatov, Bertulis, Mickene, 1997). Разница заключается в том, что мы предполагаем объединение нескольких фильтров, настроенных на разные частоты, в модули. Модули состоят из фильтров, имеющих от одной до нескольких гармоник и обрабатывающих один и тот же участок поля зрения. В первом приближении в качестве весовых функций фильтров рассматриваются синусы и косинусы, настроенные на разные частоты, заданные на одном и том же конечном промежутке и имеющие на нем несколько периодов (Глезер, 1985). По своей сути, модель модулей осуществляет разложение в конечный ряд Фурье. В работе Бондарко (1989) было показано, что модули, оптимальным образом (с наименьшей потерей информации) описывающие изображения разной формы, отличаются по размеру. Несколько модулей разной величины функционируют на одном и том же участке поля зрения. На изображение другого размера, но той же формы будет реагировать модуль с пропорциональным размером, что обеспечивает инвариантность оценки размера изображений. Модель модулей была предложена В.Д. Глезером на основании нейрофизиологических данных по изучению свойств рецептивных полей (РП) нейронов стриарной коры. Было показано, что часть РП нейронов линейна, весовые функции РП имеют до четырех возбудительных зон и подобны элементам Габора (Kulikowski, Marcelja, Bishop, 1982). Элементы Габора представляют собой синусы и косинусы, промодулированные гауссианой.
На рис. 5 показаны результаты расчетов размера промежутка в модели модулей при оптимальном описании изображений, состоящих из нескольких линий, элементами Габора. Здесь модули состоят из 1-5 гармоник. За размер модуля был взят промежуток, на котором значения гауссианы превышают уровень 10% от максимального значения. По оси абсцисс отложено количество линий в изображениях, по оси ординат - величина промежутка. Как видно из рисунка, лучшее приближение к экспериментальным кривым дают модули, состоящие из четырех или пяти гармоник. При увеличении числа гармоник в модуле максимум сдвигается в сторону увеличения числа линий. Аналогичная зависимость должна получаться и в модели Булатова, Бертулиса и Мицкене (Bulatov, Bertulis, Mickene, 1997) при увеличении чувствительности более высокочастотных фильтров. По существу, модели не сильно отличаются друг от друга. При добавлении в модуле гармоник с большим количеством периодов также добавляются фильтры, настроенные на более высокие частоты. Разница в моделях заключается в том, что у Булатова с коллегами фильтры, настроенные на одну частоту, перекрываются в пространстве. Кроме того, у них все фильтры имеют одинаковую ширину полосы пропускания. В модели модулей у фильтров с большим числом гармоник ширина пропускания уже. Один и тот же участок изображения описывает четыре фильтра, настроенных на одну и ту же частоту, но отличающихся по фазе на четверть периода. В отличие от модели Булатова и др., модель модулей дает инвариантное по отношению к величине промежутка описание. Но насколько иллюзия ОК инвариантна к размеру, так и остается открытым вопросом. Как было сказано ранее, разные исследователи получили разные результаты, изучая эту проблему. Мы в первом эксперименте получили инвариантность к размеру, а во втором и в третьем экспериментах величина иллюзии уменьшалась при увеличении ширины интервала. С чем связано такое расхождение, неизвестно. Возможно, с вариабельностью результатов в первом эксперименте, не позволившей получить достоверной зависимости от размера. Незначительное уменьшение величины иллюзии ОК с увеличением ширины интервала наблюдали и Лонг с Муртагом (Long, Murtagh, 1984).
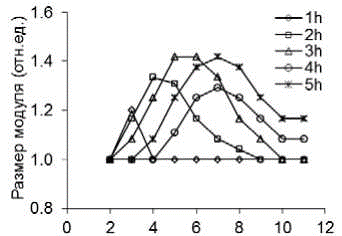
Число линий в стимуле
Рис. 5. Величина иллюзии Оппель-Кундта, рассчитанная в модели модулей:
Ось абсцисс - количество линий в стимуле. Ось ординат - размер модуля (размер пространственного интервала), при котором происходит наилучшее описание формы стимула в относительных к размеру стимула единицах. Кривая 1h -модуль состоит из одной гармоники, кривые 2-5h - из 2-5 гармоник
В пользу модели модулей высказываются и другие исследователи. Так, подобное объяснение данных по мгновенному определению количества изображений в поле зрения наличием фильтров с несколькими периодами в первичной коре (максимально с четырьмя) дают Аткинсон, Кэмпбелл и Франсис (Atkinson, Campbell, Francis, 1976) и последующие исследователи этой проблемы.
Модель, рассчитанная в настоящей работе, объясняет возникшие искажения в оценке размеров пространственных интервалов при добавлении дополнительных линий. Модель модулей разработана на основе нейрофизиологических данных (Глезер, 1985). В ней модули состоят из набора ПЧ-фильтров. Поэтому, с нашей точки зрения, объяснение искажения восприятия размеров взаимодействием между ПЧ-каналами кажется вполне допустимой, тем более что это взаимодействие на самом деле имеет место в зрительной системе. Эффектом растормаживания между ПЧ-каналами можно объяснить увеличение иллюзии в случае равноотстоящих линий в эксперименте 2.
Заключение
При добавлении дополнительных линий наблюдалась переоценка размера пространственных интервалов, которая зависела от числа линий и от их формы. Большая по величине иллюзия получена для регулярно расположенных линий и интервалов, ограниченных изогнутыми линиями. Результаты экспериментов не позволяют сделать однозначный вывод в пользу инвариантности восприятия иллюзии ОК к размеру пространственных интервалов. Инвариантная зависимость от числа линий в иллюзии Оппель-Кундта аппроксимирована моделью модулей, предполагающей обработку изображений ПЧ-фильтрами, настроенными на различные частоты и обрабатывающими один и тот же участок поля зрения. Можно заключить, что иллюзия ОК связана с обработкой изображений ПЧ-фильтрами, а также с пространственным взаимодействием между ПЧ-каналами.
[*] Бондарко В. М. Доктор биологических наук, ведущий научный сотрудник, лаборатория физиологии зрения, Институт физиологии имени И.П. Павлова РАН. E-mail: vmbond@gmail.com
[†] Бондарко Д. В. Инженер, лаборатория информационных технологий и математического моделирования, Институт физиологии имени И.П. Павлова РАН. E-mail: dmvb8@mail.ru
[‡] Чихман В. Н. Кандидат технических наук, старший научный сотрудник, заведующий лабораторией информационных технологий и математического моделирования, Институт физиологии имени И.П. Павлова РАН. E-mail: niv@pavlov.infran.ru
Литература
- Бертулис А., Булатов А., Логинович Е. Восприятие линейных размеров разных геометрических фи- гур // Сенсорные системы. 1995. Т. 9. № 1. С. 81–85.
- Бондарко В.М. Сопоставление метрик, заданных на пространстве признаков изображений, с ошиб- ками в опознании этих изображений // Сенсорные системы. 1989. Т. 3. № 1. С. 56–68.
- Бондарко В.М. Данилова М.В. Различение ширины пространственных интервалов, ограниченных двумя линиями, в условиях присутствия дополнительных боковых линий // Сенсорные системы. 1998. T. 12. С. 452–461.
- Булатов А.Н., Бертулис А.В., Мицкене Л.И. Количественное исследование геометрических иллю- зий // Сенсорные системы. 1995. Т. 9 (2–3). С. 79.
- Глезер В.Д. Зрение и мышление. Л.: Наука, 1985. 300 с.
- Глезер В.Д., Чукова С.В., Семенов Н.А., Калитиевский, Н.Ф., Бондарко В.М., Гаузельман В.Е. Различение пространственных интервалов между двумя линиями: нейрофизиологическое обоснова- ние психофизического эксперимента // Физиология человека. 1997. Т. 23. № 2. С.60–67.
- Грегори Р.Л. Глаз и мозг. М.: Прогресс, 1970. 143 с.
- Atkinson J., Campbell F., Francis M. The magic number 4 +/- 0: A new look at visual numerosity // Perception. 1976. Vol. 5. P. 335–342.
- Bondarko V.M., Danilova M.V. Spatial interval discrimination in the presence of flanking lines // Spatial Vision. 1999. Vol. 12. P. 239–253.
- Brigell M., Uhlaric J., Goldhorn P. Contextual influences on judgment of linear extent // J. Exp. Psychol.: Human Perception& Performance. 1977. Vol. 3 P. 108.
- Bulatov A., Bertulis A., Mickiene L. Geometrical illusions: Study and Modelling // Biological Cybernetics. 1997. Vol. 77. P. 395–406.
- Coren S., Girgus J. S. Seeing is deceiving: The psychology of visual illusions. Oxford, England: Lawrence Erlbaum, 1978. 255 p.
- Foley J.M., Ribeiro-Filho N.P., Da Silva J.A. Visual perception of extent and the geometry of visual space
- // Vision Research. 2004. Vol. 44. P. 147–156.
- Giora E., Gori S. The perceptual expansion of a filled area depends on textural characteristics // Vision research. 2010. Vol. 50. P. 2466–2475.
- Gogel W.C. The validity of the size-distance invariance hypothesis with cue reduction // Perception & Psychophysics. 1971. Vol. 9. P. 92–94.
- Gregory R.L. Distortion of visual space as inappropriate constancy scaling // Nature. 1963. Vol. 199. P. 678–679.
- Higashiyama A., Adachi K. Perceived size and perceived distance of targets viewed from between the legs: Evidence for proprioceptive theory // Vision Research. 2006. Vol. 46. P. 3961–3976.
- Kreiner W.A. On the intensity maximum of the Oppel-Kundt illusion [Электронный ресурс] // URL: http://d-nb.info/1060437139/34 2009( дата обращения: 22.07.2016).
- Kulikowski J.J., Marcelja S., Bishop P.O. Theory of spatial position and spatial frequency relations in the receptive fields of simple cells in the visual cortex // Biological Cybernetics. 1982. Vol. 43(3). P. 187–198.
- Hess R.F., Badcock D.R. Metric for separation discrimination by the human visual system // J. Opt. Soc. Am., A. 1995. Vol. 12. № 1. P. 3–16.
- Long G.M., Murtagh M.P. Task and Size Effects in the Oppel-Kundt and Irradiation Illusions // J. General Psychology. 1984. Vol. 111(2). P. 229–240.
- Rothwell B., Zaidel E. Visual field differences in the magnitude of the Opel-Kundt illusion vary with processing time // Perception & Psychophysics. 1990. Vol. 47. P. 180–190.
- Kisvarday Z.F., Kim D.Sh., Eysel U.T., Bonhoeffer T. Relationship between lateral inhibitory connections and the topography of the orientation map in cat visual cortex // Eur. J. Neurosci. 1994. Vol. 6. P. 1619–1632.
- Polat U. Sagi D. Lateral interactions between spatial channels: suppression and facilitation revealed by lateral masking experiments // Vision Research. 1993. Vol. 33. P. 993–999.
- Wackermann J., Kastner K. Determinants of filled/empty optical illusion: Search for the locus of maximal effect // Acta Neurobiol. Exp. 2010. Vol. 70. P. 423–434.
Информация об авторах
Метрики
Просмотров web
За все время: 2639
В прошлом месяце: 22
В текущем месяце: 14
Скачиваний PDF
За все время: 930
В прошлом месяце: 9
В текущем месяце: 0
Всего
За все время: 3569
В прошлом месяце: 31
В текущем месяце: 14